수리통계학 4. Markov’s inequality & Chebyshev’s inequality
Markov’s inequality
수리통계학에서 가장 중요한 부등식 중 하나인 마르코프 부등식(Markov’s inequality)입니다. 평균과 분산은 분포의 형태를 결정하는 중요한 요소입니다.
마르코프 부등식은 평균만을 이용해서 자료의 분포에 대해 추정합니다.
정의
Let \(u(X)\) be a nonnegative function of the random variable \(X\). If \(E[u(X)]\) exists, then \[P (u(X) ≥ c) ≤ \frac{E[u(X)]}{c}\]
for every positive constant c.
음이 아닌 확률변수 u(X)에 대해, E(u(x))가 존재하면 u(X)의 대략적인 확률을 구할 수 있습니다.
u(x)를 간단히 함숫값 \(\alpha\)로 생각하면 다음의 그림과 같이 그릴 수 있습니다.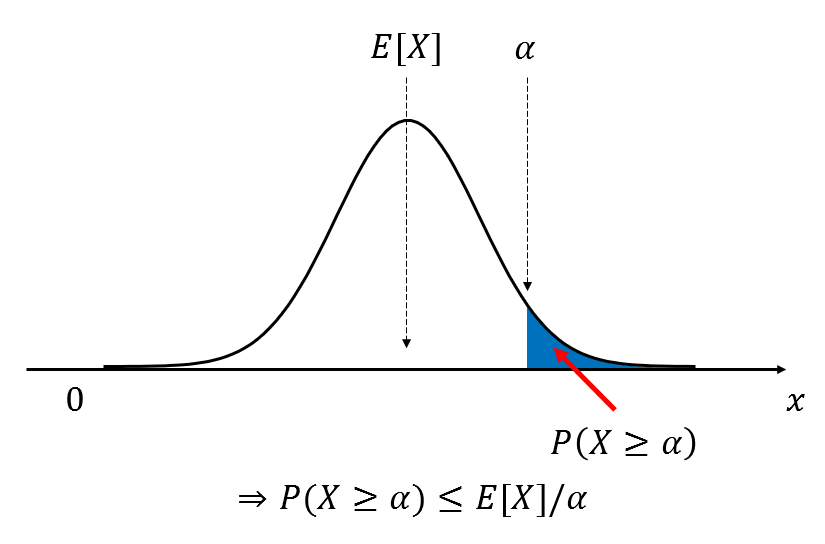 
u(x)를 확률변수로 생각하면 설명하기 좀 복잡해져서.. 편의상 이렇게 이해하는게 나을 것 같습니다.
증명
Let \(X\) be a continuous random variable and \(A=\{x:u(x)\geq c\}\). Then, \[\begin{aligned} E[u(X)] & =\int_{-\infty}^{\infty} u(x) f_X(x) d x \\ & =\int_A u(x) f_X(x) d x+\int_{A^c} u(x) f_X(x) d x \\ & \geq \int_A u(x) f_X(x) d x \\ & \geq \int_A c f_X(x) d x \\ & =c \int_A f_X(x) d x \\ & =c P(X \in A) . \end{aligned}\]
X의 기댓값 E(X)는 \(\int xf(x) dx\) 로 구합니다. 이 \(x\)의 자리에 \(u(x)\)를 넣어줬다고 이해할 수 있습니다. u(x)가 임의의 양수 c보다 크다는 조건이 있기 때문에 4번째 줄의 식이 성립합니다. 확률밀도함수에서 c보다 큰 구간의 확률의 최소값이 \(\int_A c f_X(x) dx\)으로 주어지기 때문에 대략적으로 확률을 추정할 수 있는 것입니다.
Chebyshev’s inequality
마찬가지로 통계학에서 중요한 부등식입니다. 이 부등식을 증명하기 위해 위의 Markov’s inequality를 사용합니다. 체비셰프 부등식은 평균만 활용하여 확률을 추정했던 마르코프 부등식과 달리 평균과 분산을 함께 활용하여 더욱 정확한 추정이 가능하게 합니다.
정의
Let the random variable X have a probability distribution about which we assume only that there is a finite variance \(σ^2\). Then for every k>0, \[P(|X-\mu|\geq k\sigma)\leq \frac{1}{k^2}\]
or, equivalently, \[P(|X-\mu|< k\sigma)\geq 1-\frac{1}{k^2}\]
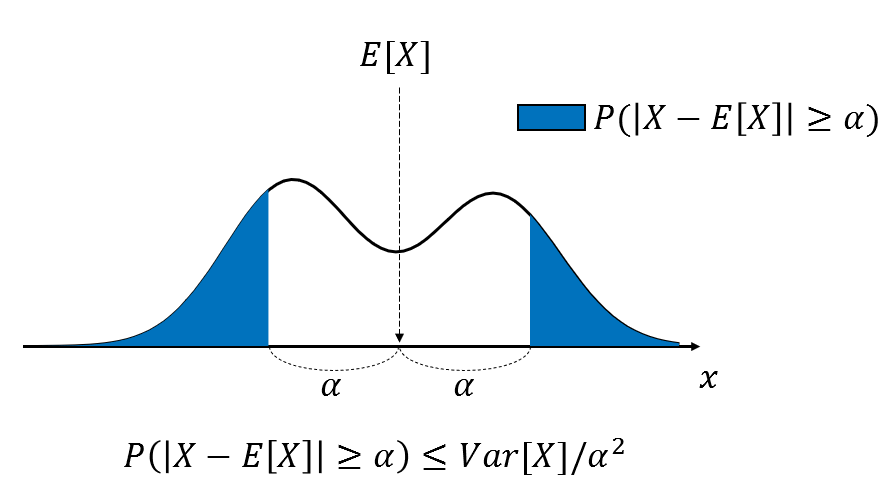위의 그림은 \(k\sigma\)를 임의의 상수 \(\alpha\)로 두고 있습니다.
임의의 분포를 따르는 X라는 확률변수를 가정합니다. 이를 \(X \sim \cdot\left(\mu, \sigma^2\right)\)로 표현할 수 있습니다. \(|X-\mu|\), 즉 X와 \(\mu\) 사이의 거리가 표준편차와 k의 곱보다 클 확률이 \(\frac{1}{k^2}\)이하(그렇게 크지 않다)라는 사실을 나타내고 있습니다.
다시 말해서, 체비셰프 부등식은 전체 데이터 분포에서 기댓값(평균)을 기준으로 확률변수 X가 어떤 양쪽 극값 \(E(X) \pm \alpha\)보다 크거나 작은 확률에 관한 것입니다.
변형식이 훨씬 유용하게 사용된다고 합니다.
증명
From the Markov’s inequality, we take \(u(X) = (X − μ)^2\) and \(c = k^2σ^2\). Then we have \[\begin{aligned} P(u(X) \geq c) & \leq \frac{E[u(X)]}{c} \\ P\left((X-\mu)^2 \geq k^2 \sigma^2\right) & \leq \frac{E\left[(X-\mu)^2\right]}{k^2 \sigma^2} \\ P(|X-\mu| \geq k \sigma) & \leq \frac{\operatorname{Var}(X)}{k^2 \sigma^2}=\frac{1}{k^2} \end{aligned}\]
풀어서 설명해보면, 우선 \(u(X) = (X − μ)^2\) and \(c = k^2σ^2\)로 가정하고 이를 마르코프 부등식에 대입합니다. 대입을 완료하면 2번째 줄의 식이 나올 것입니다. 여기서 \(E\left[(X-\mu)^2\right]\)는 분산(\(\sigma^2\))의 정의와 같습니다. 그러면 시그마 제곱이 약분되어 최종적으로는 \(\frac{1}{k^2}\)만 남을 것입니다.
실제로는 모평균과 모분산을 알기 어려운 경우가 많으므로, 부등식을 활용할 땐 표본평균과 표본분산을 사용해도 무방하다고 합니다.
예시
\(\begin{aligned} & k=2, \\ & =P(|x-\mu|<2 \sigma) \\ & =P(-2 \sigma+\mu<x<2 \sigma+\mu) \geq 1-\frac{1}{4}=\frac{3}{4} \end{aligned}\)
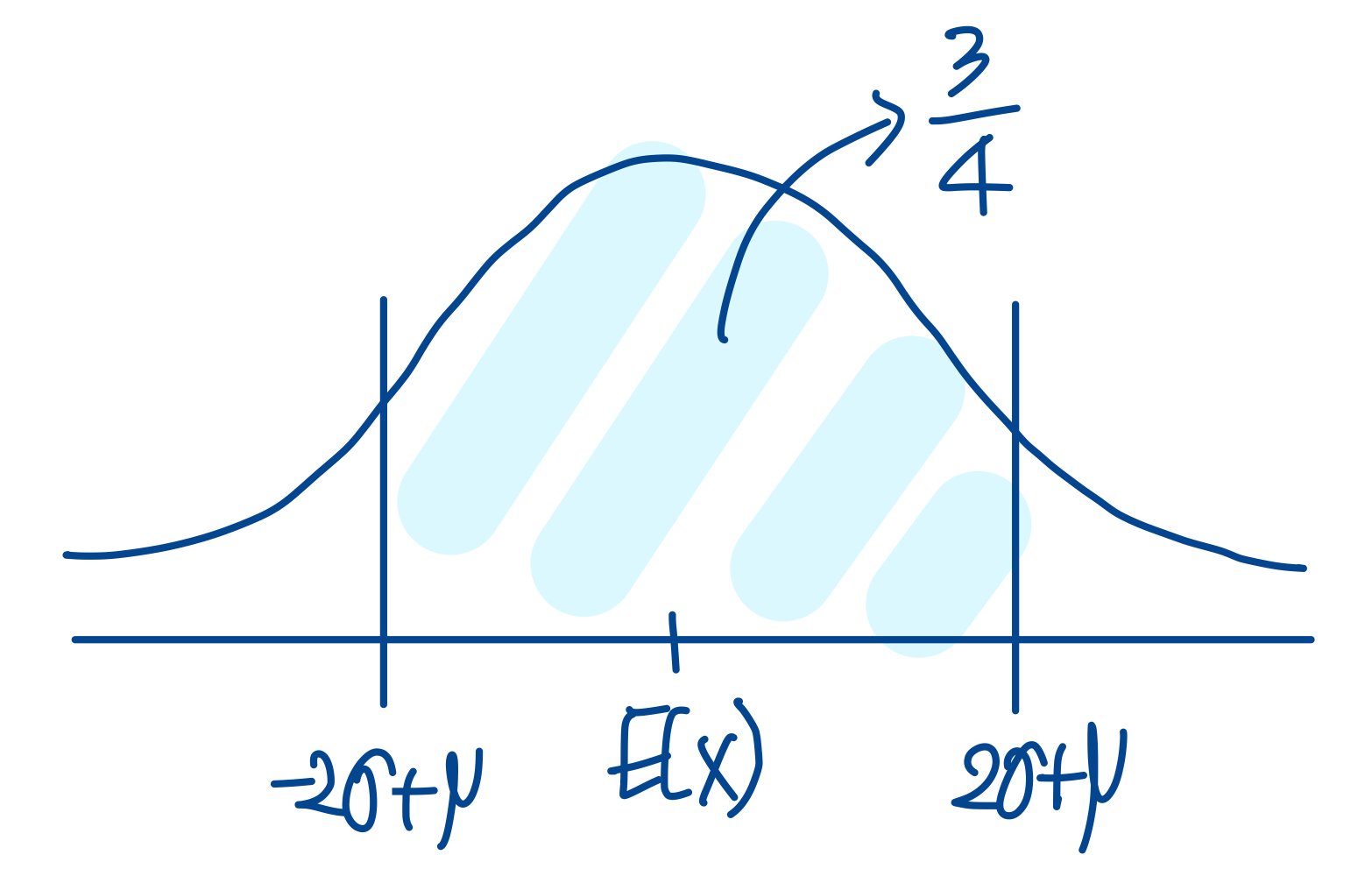k가 2일때 \((-2\sigma+\mu, 2\sigma+\mu)\) 구간의 확률은 최소 0.75라는 것을 알 수 있습니다.
이미지 출처: https://angeloyeo.github.io/2022/09/12/Markov_Chebyshev_Inequality.html#google_vignette
