Stat3
수정해야함
수리통계학 2. Various Distributions
Probability Distribution
오늘은 통계학에서 흔히 다뤄지는 확률분포들에 대해서 다뤄보겠습니다.
Bernoulli Distribution
결과가 (1, 0) 두 가지 중 하나로만 나오는 실험이나 시행을 Bernoulli Trial이라고 합니다.
동전 던지기가 예시입니다. 베르누이 분포를 따르는 확률변수는 X~Ber(𝜇)로 표기합니다.
1이 나올 확률 𝜇와 0이 나올 확률 1-𝜇이 주어졌을 경우, x=0, x=1를 대입하여 각각의 확률을 계산할 수 있습니다. \[P(x \mid \mu)=\mu^x(1-\mu)^{1-x}, \quad \mathbb{E}[X]=\mu, \quad \mathbb{V}[X]=\mu(1-\mu)\]
x=0의 확률, x=1의 확률이라고 생각하면 굉장히 쉽습니다.
Binomial Distribution
성공확률이 𝜇인 베르누이 시행을 N번 반복하고, 성공한 횟수가 x번인 사건에 해당합니다. 이항분포를 따르는 확률변수는 X~B(x; N, 𝜇)로 표기합니다. \[P(m \mid n, \mu)=\left(\begin{array}{c} n \\ m \end{array}\right) \mu^m(1-\mu)^{n-m}, \quad \mathbb{E}[Y]=n \mu, \quad \mathbb{V}[Y]=n \mu(1-\mu)\]
Poisson Distribution
푸아송 분포는, 단위 시간 안에 어떤 사건이 몇 번 발생할 것인지를 표현하는 이산확률분포입니다. 예를 들어, 1시간 동안 회사A에 전화가 오는 횟수 / 1분 동안 가게에 오는 손님의 명수 등으로 생각할 수 있습니다. 단위시간을 사용한다는 사실이 조금 추상적이고 애매하게 느껴질 수는 있지만, 단순하게 생각하면 오히려 이해가 잘 될수도 있습니다 !
다시 예시를 들어서, 주중 오후에 1시간동안 가게에 오는 손님이 몇 명인지 알고 싶습니다. 평균적으로 4분마다 3.2명의 손님이 온다고 가정합니다. 그러면 주중 오후에 가게에 4분동안 정확히 5명의 손님이 올 확률은 얼마일까요?
1분을 기준으로 한다면 1시간은 60분, 즉 60번의 사건이 시행됩니다.
4분마다 3.2명, 즉 1분에 0.8명이 오기 때문에 사건발생확률은 0.8입니다.
우선 이 사건은 두 분포로 접근할 수 있습니다.
1) 이항분포
\(B(n, p ; k)=B(60,0.8 ; 5)=\frac{60 !}{5!(60-5) !}(0.8)^5(0.2)^{60-5}\)
그런데 여기서 60!나 0.2의 55승 같은 수는 너무 커서 계산하기가 어렵습니다.
이처럼 이항분포에서 n이 너무 크고 p가 너무 작은 경우, 이항분포의 확률분포를 근사적으로 계산하는 분포가 푸아송 분포입니다.
2) 푸아송 분포
푸아송 분포의 유일한 parameter는 \(\lambda\)입니다.
푸아송 분포를 따르는 확률변수는 \(X \sim Pois(\lambda)\)로 표기합니다. 이 람다값은 단위시간 동안 사건이 일어나는 평균 확률이며, 하나의 사건을 다루는 분포에서 일정하게 유지됩니다. x값은 사건의 발생 횟수를 의미합니다. \[P(x)=\frac{\lambda^x e^{-\lambda}}{x !}\]
그러면 이제 위의 문제를 푸아송 분포로 풀어보겠습니다. 단위시간이 4분이기 때문에 0.8로 바꿔줄 필요 없이, 람다값은 3.2로 설정하겠습니다. \[P(x=5)=\frac{\lambda^5 e^{-\lambda}}{5!}=\frac{3.2^5 e^{-3.2}}{5!}\]
파이썬으로 계산해 보겠습니다.
from math import exp, factorial
lambda_ = 3.2
k = 5
P_k_lambda = (lambda_**k*exp(-lambda_))/factorial(k)
P_k_lambda
최종적으로 0.114 의 확률이 나옵니다.
비슷한 예시로, 토요일 아침에는 10분마다 2.4명의 손님이 온다고 합니다. 토요일 아침에 6분동안 2명의 손님이 올 확률은 얼마일까요?
1분마다 0.24명의 손님이 오는 것이므로 6분이면 1.44명입니다. 람다값은 1.44로 설정합니다. 이 단위시간 동안 2명의 손님이 오는 것이기 때문에 P(x=2)를 구할 것입니다. \[P(x=2)=\frac{\lambda^2 e^{-\lambda}}{2!}=\frac{1.44^2 e^{-1.44}}{2!}\]
from math import exp, factorial
lambda_ = 1.44
k = 2
P_k_lambda = (lambda_**k*exp(-lambda_))/factorial(k)
P_k_lambda
최종적으로 0.246 의 확률이 나옵니다.
HyperGeometric Distribution
초기하분포는 이항분포와 유사하게 (0,1) 두 가지의 결과만이 존재합니다.
하지만, 이항분포와 달리 초기하분포는 비복원 추출입니다. 즉 초기하분포는 비복원추출에서 N개의 모집단 중 n개를 추출할 때, k번의 성공을 할 확률에 대한 분포입니다. 비복원추출이라는 특징은 앞선 시행이 다음 시행의 확률에 영향을 준다는 점에서 중요한 역할을 합니다.
초기하분포의 또다른 특징은, 바로 모집단이 유한하다는 점입니다.
초기하분포에서는 모집단의 크기가 고정되어 있고, 추출되는 표본의 크기에 따라 성공 확률이 변할 수 있습니다. 따라서 초기하분포에서는 모집단의 크기와 함께 모집단에서의 성공 확률을 알아야 합니다.
우리가 평소에 다루던 이항분포는 모집단의 크기가 무한대에 가깝다고 가정하고, 각 시행이 서로 독립적이며 성공 확률이 일정하다고 가정했습니다. 모집단의 크기가 고려되지만, 모집단에서의 성공 확률은 몰라도 되는 것입니다. 대신 표본의 크기와 성공 횟수만으로 이항분포를 계산할 수 있습니다. \[P(x)=\frac{{ }_A C_x \cdot{ }_{N-A} C_{n-x}}{{ }_N C_n}\]
N=모집단의 크기, n=표본의 크기, A=모집단에서의 성공 횟수, x=표본에서의 성공 횟수 입니다.
예시를 들어보겠습니다.
24명의 학생이 있는데, 이중 8명이 매운 음식을 먹지 못합니다. 24명의 학생들 중 5명을 랜덤하게 선택했을 때, 선택된 학생 중 3명이 매운 음식을 먹지 못할 확률은 무엇일까요?
우선 N=24, n=5, A=8, x=3으로 설정해야 합니다. 이 값을 모두 대입하면 다음과 같은 식을 얻을 수 있습니다. \[P(x=3)=\frac{{ }_8 C_3 \cdot{ }_{16} C_{2}}{{ }_{24} C_5} =0.1581\]
이 예시가 비복원추출인 이유는, 한 번 선택된 학생은 다시 선택되지 않기 때문입니다.
이항분포에 적용하려면 각 시행이 독립적이어야 하므로, 학생이 모두 같은 확률로 매운 음식을 먹지 못해야 합니다. 반면 초기하분포에서는 매운 음식을 먹을 수 있는 학생과 그렇지 못한 학생이 이미 정해져 있습니다.
이항분포에서 학생이 매운 음식을 먹지 못할 확률을 0.33으로 가정할 때 표본으로 선택되는 5명 중 3명이 매운 음식을 먹지 못할 확률은, \[P(x=3)=\left(\begin{array}{l} 5 \\ 3 \end{array}\right)(0.33)^3(0.67)^2=0.1613\]
과 같이 계산할 수 있습니다. 여기서 식을 보면, 모집단의 크기는 고려되지 않는 것을 확인할 수 있습니다. 성공 확률만 알고 있다면 정확한 모집단의 크기는 알지 않아도 확률을 계산할 수 있는 것입니다.
Gaussian Distribution
가우시안 분포는 “정규 분포(Normal Distribution)”라는 이름으로 연속확률분포 중 가장 널리 쓰이는 확률분포입니다.
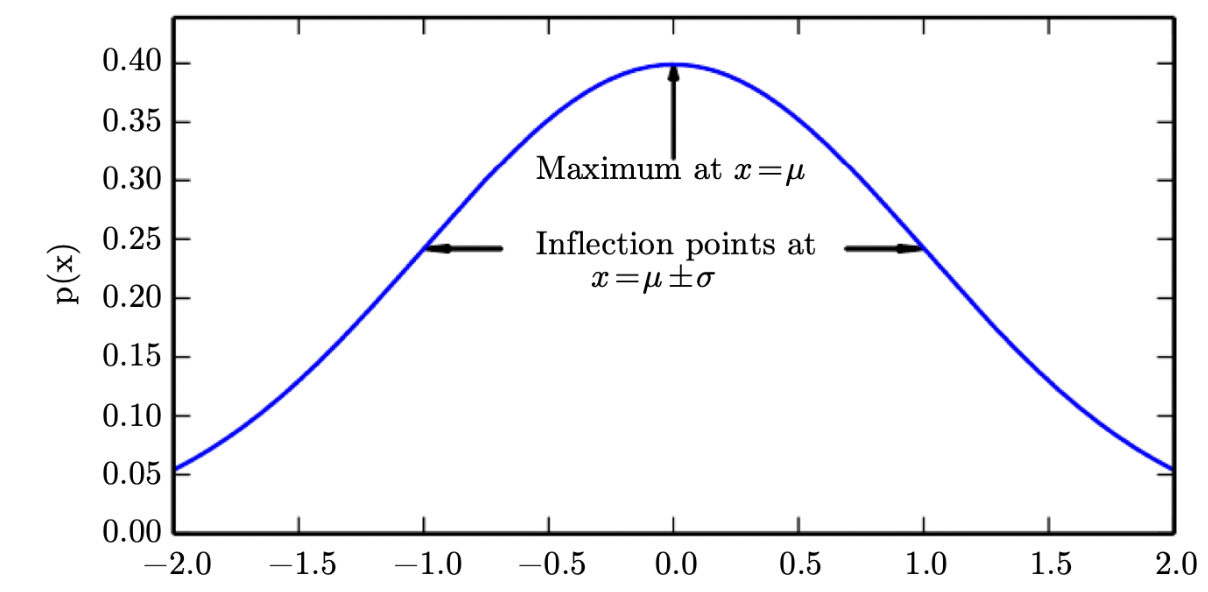
특징
- 평균(\(\mu\))과 표준편차(\(\sigma\))에 의해 형태가 결정됩니다.
- 평균을 기준으로 좌우가 대칭(symmetric)입니다.
- x축이 점근선(asymptotic)입니다.
- 단봉형(unimodal)입니다.
- aX ~ N(a𝜇, a^2𝜎^2)
가우시안 분포의 확률밀도함수는 다음과 같습니다. (암기할 필요는 없습니다) \[p\left(X \mid \mu, \sigma^2\right)=\frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left(-\frac{(X-\mu)^2}{2 \sigma^2}\right)\]
이 정규분포를 표준화한 표준정규분포(Standardized Normal Distribution)도 자주 다루게 됩니다.
모든 정규분포는 표준화될 수 있는데, 이를 z분포(표준정규분포)라고 부릅니다.
다음의 공식을 통해 분포를 표준화할 수 있습니다. \[Z=\frac{X-\mu}{\sigma}\sim N(0,1^2)\]
z score라고 부르는 이 z값은 평균이 0이고 표준편차가 1인 정규분포를 따릅니다. z score는 주어진 x값이 평균으로부터 몇 개의 표준편차만큼 떨어져 있는가를 나타냅니다.
예시를 들어보겠습니다. 정규분포를 따르는 확률변수 X가 \(X \sim N(2, 3^2)\)일 때, X가 5보다 큰 부분의 확률을 구하려면 다음과 같이 계산할 수 있습니다. \[P(X \geqslant 5)=P\left(\frac{X-2}{3}=Z \geqslant 1\right)\]
우리는 분위수(Quantile)를 이용해 표준정규분포의 특정 영역의 넓이(전체 넓이는 1)와 이에 해당되는 z score를 구할 수 있습니다. 자주 쓰이는 분위값은 아래와 같습니다.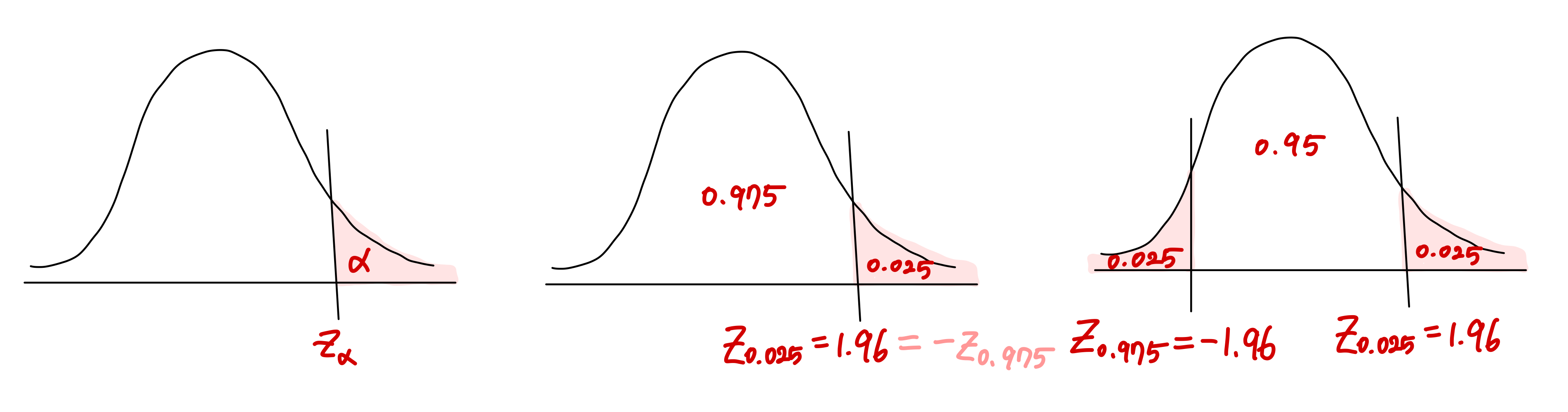 
\[z_{0.025}=1.96, z_{0.95}=-z_{0.05}=-1.645, z_{0.975}=-z_{0.025}=-1.96\]
Exponential Distribution
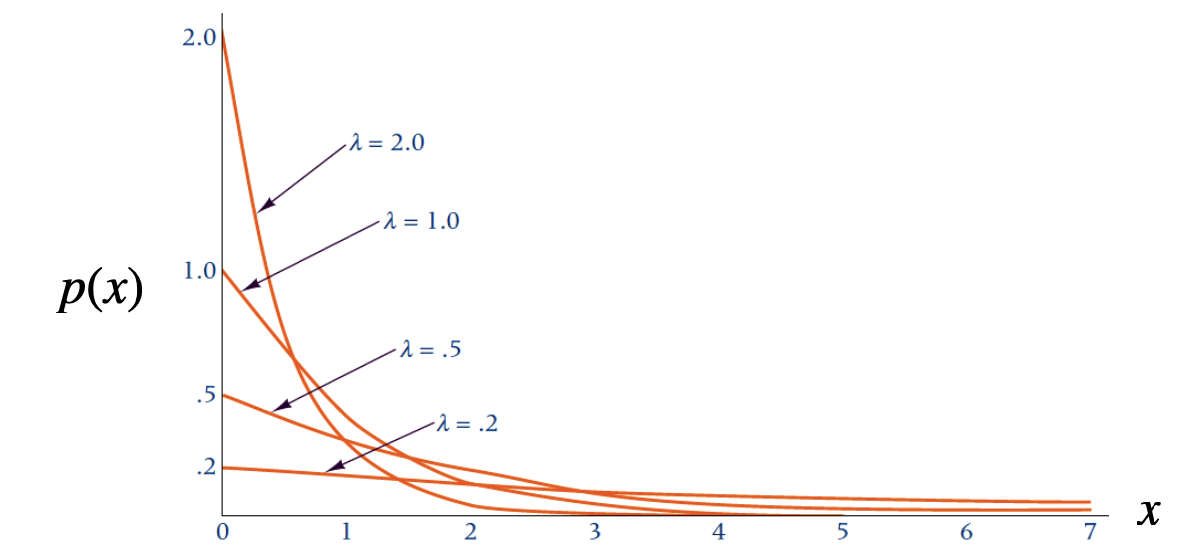
지수분포입니다. 우리가 앞서 살펴보았던 초기하분포는 이 지수분포의 특수한 경우라고 볼 수 있습니다. 초기하분포는 단위시간 동안 발생하는 사건의 횟수(# of events occurred in unit time)를 나타낸 분포였습니다. 지수분포는 같은 상황에서 다음 사건이 일어날 때까지의 대기시간, 예를 들면 다음 손님이 올 때까지의 소요시간(inter-arrival time of different customers)을 나타내는 확률분포입니다. 현실에서의 문제에 적용해보면, 은행 창구에서 평균 대기시간, 고장과 관련된 기계의 수명 등을 모형화하는데에 적합할 것입니다. X~Exp(λ)로 표기합니다. 람다값은 단위 시간동안 사건 발생횟수를 의미하며, 지수분포의 형태를 결정합니다.
지수분포의 PDF는 다음과 같습니다. \[p(x)=\lambda e^{-\lambda x} \text {, where } x \geq 0\]
특징
- \[\mu=1 / \lambda, \sigma=1 / \lambda\]
- \[E(X)=\int_0^{\infty} x \lambda e^{-\lambda x} d x=\frac{1}{\lambda}\]
- 1분에 5명이 온다고 하면 평균 대기시간은 1/5분일 것입니다.
- \(\operatorname{Var}(X)=E\left(X^2\right)-E(X)^2=\frac{2}{\lambda^2}-\frac{1}{\lambda^2}=\frac{1}{\lambda^2}\)
- CDF: \(P\left(x \geq x_0\right)=e^{-\lambda x_0}\)
- 누적분포함수는 로그함수의 형태입니다.
예시 은행에 오는 고객의 수는 람다값이 1.2인 푸아송 분포로 나타낼 수 있습니다. 매분 1.2명의 고객이 온다는 것을 의미합니다. 도착 시간 사이의 평균 시간은 무엇이며, 한 도착과 또다른 도착 사이의 소요시간이 적어도 2분이 걸릴 확률은 얼마일까요?
먼저, 해당 지수분포의 평균은 1/λ, 즉 \(\frac{1}{1.2}\approx0.833\)가 될 것입니다. 우리는 대기시간이 적어도 2분이 넘게 걸리는 문제를 풀고 싶기 때문에, 다음과 같은 식의 확률을 구해야 합니다. \(P\left(x \geq 2\right)=e^{-2\lambda}\)
람다값을 대입하면, \(e^{-2.4}\approx 0.0907\)값을 확률로 구할 수 있습니다.
따라서, 도착 대기시간이 적어도 2분이 걸릴 확률은 9.07%입니다.
Gaussian Distribution
가우시안 분포는 “정규 분포(Normal Distribution)”라는 이름으로 연속확률분포 중 가장 널리 쓰이는 확률분포입니다.
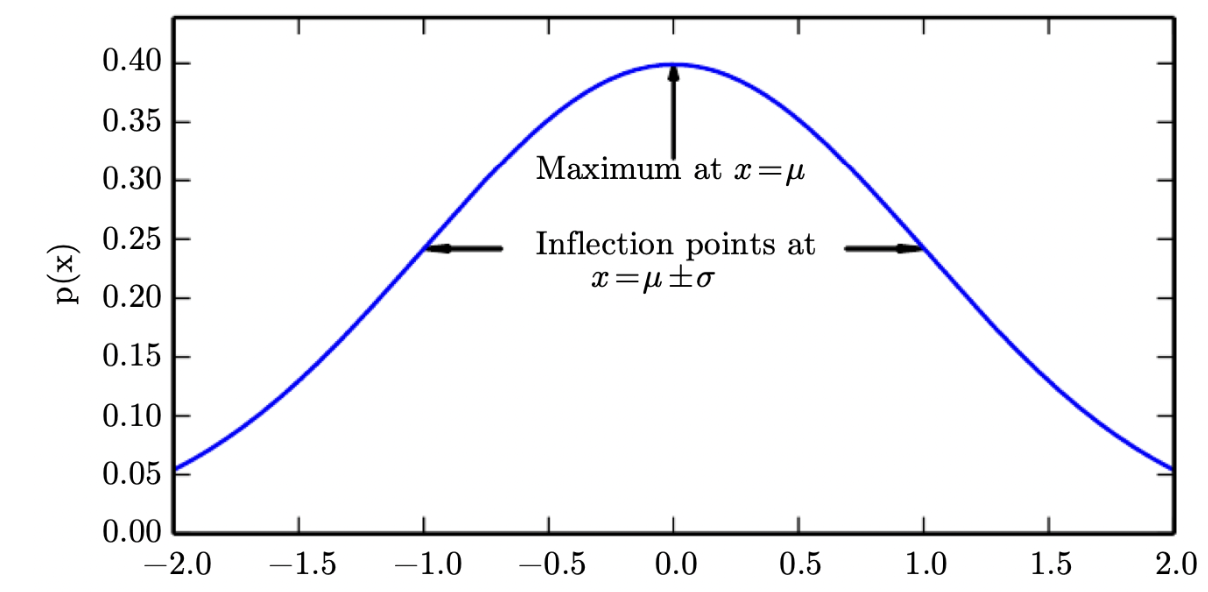
특징
- 평균(\(\mu\))과 표준편차(\(\sigma\))에 의해 형태가 결정됩니다.
- 분산이 커지면 평균을 기준으로 더 넓게 퍼지고, 분산이 작아지면 평균을 기준으로 더 모이게 됩니다.
- 평균을 기준으로 좌우가 대칭(symmetric)입니다.
- x축이 점근선(asymptotic)입니다.
- 단봉형(unimodal)입니다.
- \[aX \sim N(a\mu, a^2\sigma^2)\]
가우시안 분포의 확률밀도함수는 다음과 같습니다.(암기할 필요는 없습니다) \[p\left(X \mid \mu, \sigma^2\right)=\frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left(-\frac{(X-\mu)^2}{2 \sigma^2}\right)\]
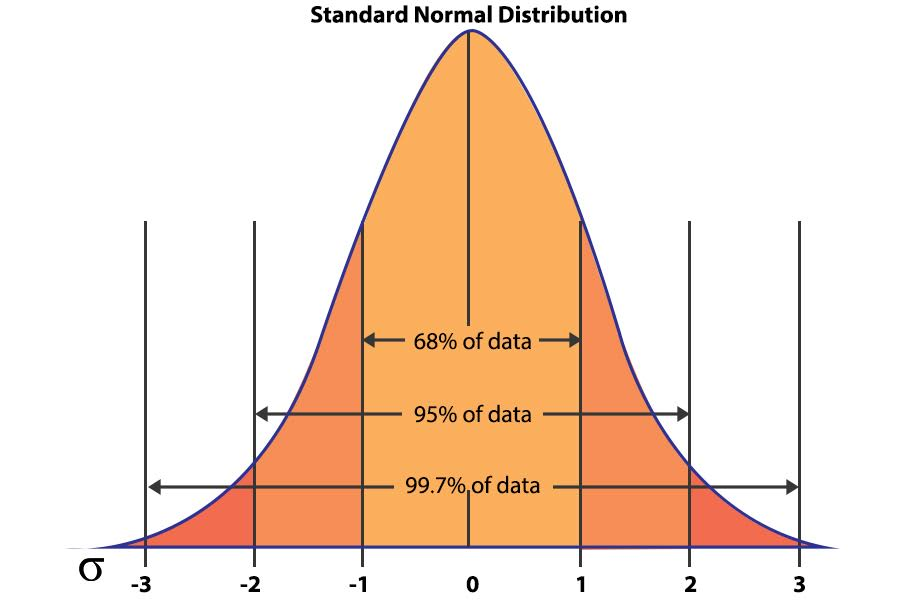
Standard Normal Distribution
위의 정규분포를 표준화한 표준정규분포(Standard Normal Distribution)도 자주 다루게 됩니다.
모든 정규분포는 표준화될 수 있는데, 이를 z분포(표준정규분포)라고 부릅니다.
다음의 공식을 통해 분포를 표준화할 수 있습니다. \[Z=\frac{X-\mu}{\sigma}\sim N(0,1^2)\]
z score라고 부르는 이 z값은 평균이 0이고 표준편차가 1인 정규분포를 따릅니다. z score는 주어진 x값이 평균으로부터 몇 개의 표준편차만큼 떨어져 있는가를 나타냅니다.
예시를 들어보겠습니다. 정규분포를 따르는 확률변수 X가 \(X \sim N(2, 3^2)\)일 때, X가 5보다 큰 부분의 확률을 구하려면 다음과 같이 계산할 수 있습니다. \[P(X \geqslant 5)=P\left(\frac{X-2}{3}=Z \geqslant 1\right)\]
우리는 분위수(Quantile)를 이용해 표준정규분포의 특정 영역의 넓이(전체 넓이는 1)와 이에 해당되는 z score를 구할 수 있습니다. 자주 쓰이는 분위값은 아래와 같습니다.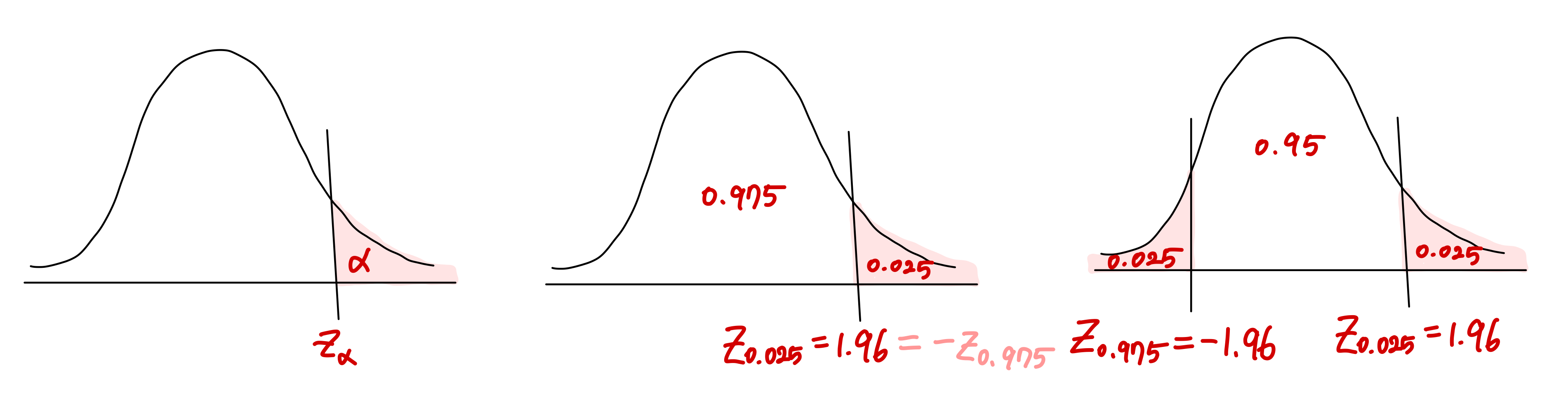 
\[z_{0.025}=1.96, z_{0.95}=-z_{0.05}=-1.645, z_{0.975}=-z_{0.025}=-1.96\]
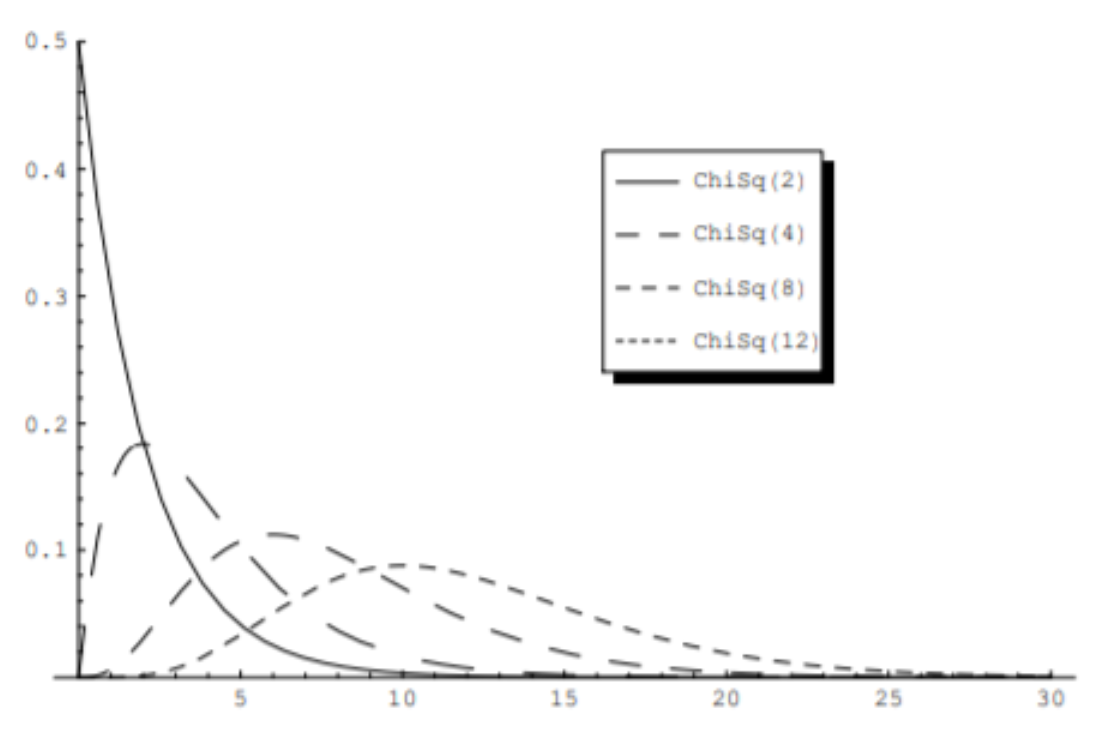
Chi-Squared Distribution
\[f_Y(y)=\frac{1}{2^{n / 2} \Gamma(n / 2)} y^{n / 2-1} e^{(-y / 2)}, \quad y \geq 0\]
기본적으로 오른쪽으로 꼬리가 긴(right-skewed) 분포입니다.
- 자유도(n)에 의해 형태가 결정됩니다.
- 자유도가 작을수록 비대칭이 되고, 자유도가 클수록 대칭에 가까워집니다.
- n개의 standard normal distribution의 확률변수들의 제곱의 합이 자유도가 n인 카이제곱분포를 따르게 됩니다.즉, \(Y=Z_1^2+\cdots+Z_n^2\)일 때 \(Y \sim \chi_n^2\)입니다.
- \(Y \sim \chi_n^2\)일 때 E(Y)=n, Var(Y)=2n입니다.
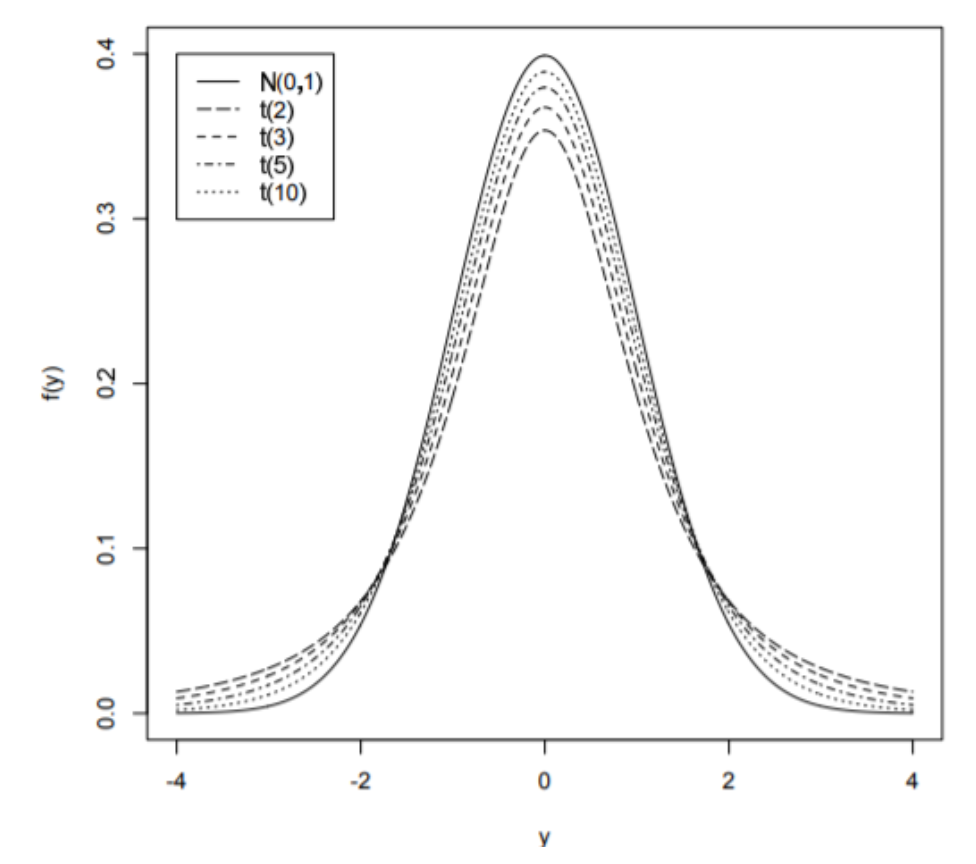
t-Distribution
\[f_Y(y)=\frac{\Gamma\{(n+1) / 2\}}{\sqrt{n \pi} \Gamma(n / 2)}\left(1+\frac{y^2}{n}\right)^{-(n+1) / 2}, \quad-\infty<y<\infty\]
정규분포에서 좀 더 두꺼운 꼬리를 가진 형태입니다. uncertain values를 다룰 때 정규분포보다 더 적합하다고 합니다. 표본평균을 이용해 정규분포의 평균을 해석할 때 많이 사용됩니다.
- 자유도(n)에 의해 형태가 결정됩니다.
- 자유도가 높을수록 정규분포에 가까워집니다.
- 대칭이고 종 모양을 띱니다.
- \(T \sim t_n\)일 때, E(T)=0, Var(T)=n/n-2 (n>2) 양의 무한대 (n<=2) 입니다.
- t분포의 확률변수 T는 \(T=\frac{Z}{\sqrt{V / n}} \sim t_n\) 로 결정될 수 있습니다.
- Z는 표준정규분포
- V는 자유도가 n인 카이제곱 분포
- Z와 V는 독립
F-Distribution
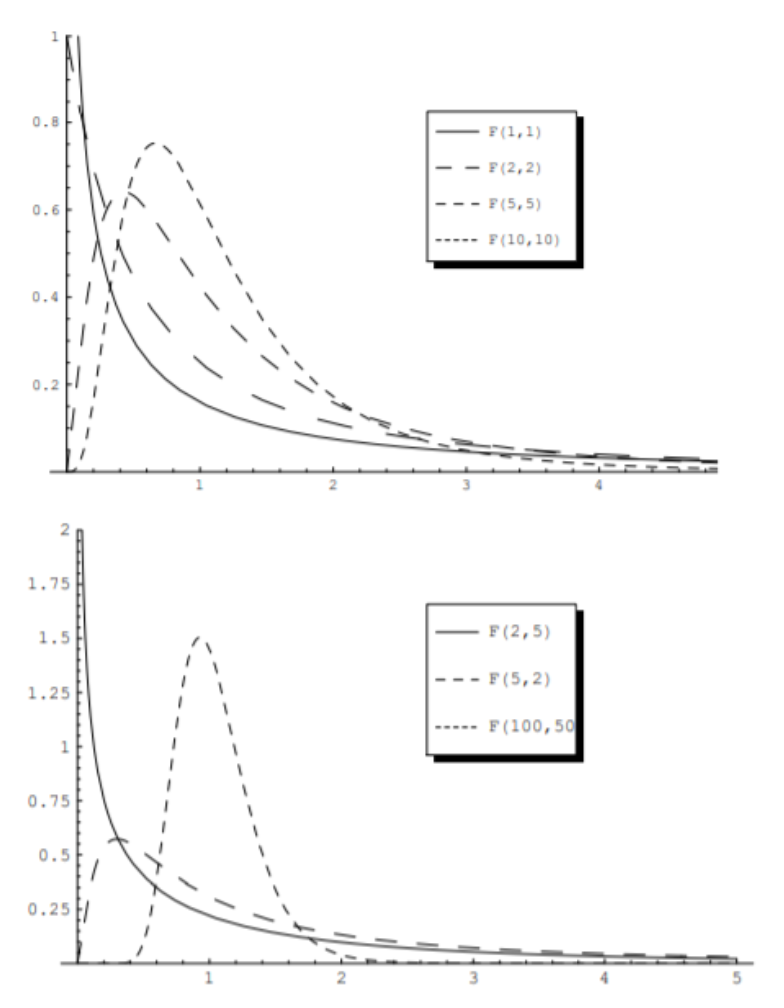
F분포는 두 확률분포의 분산의 비율에 대한 분포입니다. \[f_Y(y)=\frac{\Gamma\{(m+n) / 2\}}{\Gamma(m / 2) \Gamma(n / 2)} \frac{m}{n} y^{m / 2-1}\left(1+\frac{m}{n} y\right)^{-(m+n) / 2}, \quad y>0\]
- 자유도(m, n)에 의해 형태가 결정됩니다. 두 확률분포의 분산 비율에 대한 분포이기 때문에 각 분포의 자유도 두 개가 parameter가 됩니다. (*m과 n의 순서를 고려해야 합니다.)
- W와 X가 각각 자유도가 m, n인 독립인 카이제곱 확률변수라고 할 때, F분포의 확률변수는 다음과 같이 정의될 수 있습니다.
- If $X \sim F_{m, n}$ then $X^{-1} \sim F_{n, m}$
- If $X \sim F_{m, n}$ then $Y=\lim _{n \rightarrow \infty} m X \sim \chi_m^2$
- If $X \sim t_n$ then $X^2 \sim F_{1, n}$
03.19 update completed
