수리통계학 1. Intro
Probability and Distributions
표본공간; Sample Space
collection of every possible outcome of the experiment.
ex. {H, T}
Random Experiment
조건
1. The sample space can be described prior to its performance.
사건이 이루어지기 전에 표본공간이 결정되어야 합니다.
2. The experiment can be repeated under the same conditions.
같은 조건 하에서 반복될 수 있어야 합니다.
수리통계학 수업을 예로 들 수 있습니다.
수업을 수강하여 학점을 받는 것이 하나의 사건이면, 학생은 수업을 여러 번 들을 수 있습니다. 표본공간은 {A+, A0, A-, …} 가 될 것입니다.
하지만 초수강과 재수강, 재재수강의 조건은 다릅니다. 부여되는 학점도 이에 영향을 받을 것이므로 이 사건은 random experiment가 되지 못합니다.
subjectivity는 random experiment가 될 수 없게 하는 또 하나의 요소입니다.
ex. 내기와 같이, 같은 사건에 대해 두 인물이 다른 의견을 가지고 참여할 경우 사건의 확률이 달라질 수 있습니다.
random experiment example
1) tossing a coin
2) rolling a dice
Notation
Ω = sample space of an experiment
s = an element of Ω
C = a collection of elements of Ω, i.e., an event
Relative Frequency
ex. tossing a coin
Ω = {H, T}
C = {H}
표본공간 Ω이 N번 반복(사건 발생), C는 f번 발생
consider the ratio : \(\frac{f}{N}\) = relative frequency
N이 무한대로 증가하면, \(\frac{f}{N}\)은 p로 수렴합니다.
이때 p는 C의 probability(확률)이라 불립니다.
p는 \(\frac{C 원소 개수}{Ω 원소 개수}\)라고 정의될 수 있습니다.
확률변수; Random Variables
: numerical quantity that varies at random. 즉, “확률”적으로 결정되는 변수입니다. Discrete Random Variable과 Continuous Random Variable로 나뉩니다.
Discrete Random Variable
이산확률변수는 countable한 확률변수입니다.
예를 들면, 학생의 수, 전구의 개수 등이 있습니다.
Continuous Random Variable
연속확률변수는 uncountable한 확률변수입니다.
예를 들면, 학생의 몸무게, 키 등이 있습니다.
확률함수; Probability Functions
: mathematical function that provides probabilities for the possible outcomes of the random variable X. It is typically denoted as \(f_X(x)\).
확률변수의 분포를 나타내는 함수입니다.
확률질량함수; PMF(Probability Mass Function)
discrete random variable의 분포입니다. \[f_X(x) = P(X = x)\]
확률질량함수는 각 변수에 확률이 할당되어 있을 것입니다.
- \(f_X(x) > 0\) for x in the sample and 0 otherwise
각 변수의 확률은 0 또는 양수입니다. - \(\sum_xf_X(x) = 1\). In other words, the sum of all the probabilities of all the possible outcomes of an experiment is equal to 1.
변수별 확률의 총합은 항상 1이 됩니다.
확률밀도함수; PDF(Probability Density Function)
continuous random variable의 분포입니다.
이산확률변수와 달리 연속확률변수는 변수를 범위로 나타냅니다.
우리는 이 변수를 셀 수 없기 때문에, 확률을 넓이의 개념으로 접근하게 됩니다.
아래 그래프에서 주황색 부분의 넓이가 곧 해당 범위의 확률입니다. \[P(a<X<b) = \int ^b_a f_X(x)dx\]
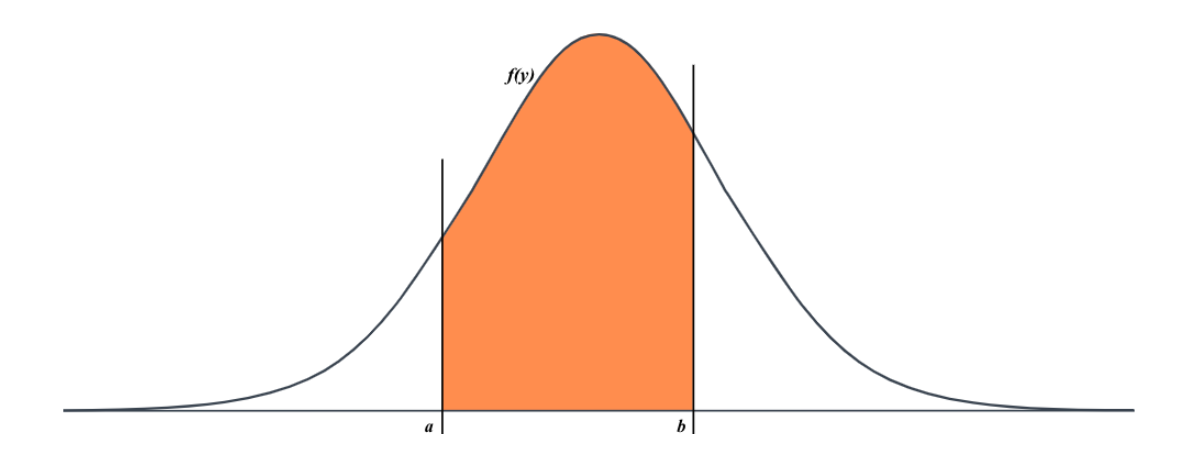
- \(f_X (x) > 0\) for x in the sample and 0 otherwise
- The area under \(f_X(x) > 0\) is equal to 1.
- \(P(X=x)=0\) for any x.
이 부분이 중요한데, 변수를 범위가 아닌 하나의 값(point)으로 지정한다면, 넓이로 확률을 다루는 PDF에서는 아무 범위도 선택되지 않습니다. 따라서 이 경우 확률은 0이 됩니다.
누적분포함수; CDF(Cumulative Distribution Function)
확률변수의 누적된 확률을 결과값으로 하는 함수입니다. \[F_x(x)=P_x((-\infty,x])= P({c\in \mathcal{C}: X(c)<x})\]
하한값은 0이고 상한값은 1이며, 값이 누적되기 때문에 오른쪽 연속 그래프라는 특징을 가집니다.
또한, 연속확률변수의 경우에서 CDF를 미분하면 PDF가 나옵니다.
그래프 정리
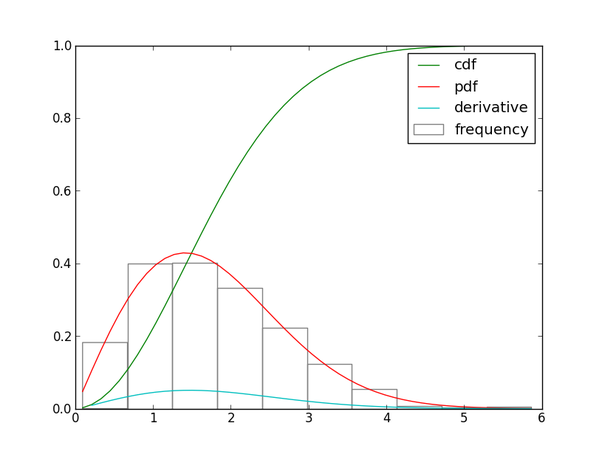회색 히스토그램이 PMF, 빨간 그래프가 PDF, 녹색 그래프가 (연속확률변수의) CDF입니다.
기댓값; Expectation
\(E(X), μ(X)\)로 표기합니다. 우리는 기댓값을 평균이라고 부르기도 합니다. \[\begin{aligned} \mathrm{E}(X) & =\sum_x x f_X(x) \quad \text { (discrete RV) } \\ & =\int_{-\infty}^{\infty} x f_X(x) d x \quad \text { (continuous RV) } \end{aligned}\]
a, b가 상수이고 X, Y는 확률변수일 때, \[E(a)=a \\ E(aX+b)=aE(X)+b \\ E(X+Y)= E(X)+E(Y) \\ E(XY)=E(X)*E(Y)\]
과 같은 성질을 가집니다. 상수의 기댓값은 상수 그 자체의 값이 그대로 나온다는 것이 중요합니다.
Notation
i.i.d. 라는 표현이 굉장히 자주 나올텐데요, 이는 independent and identically distributed(독립항등분포)의 줄임말입니다. 독립적이고, 같은 확률분포를 가진다는 뜻으로 통계학에서 가장 많이 쓰는 가정 중 하나입니다. 주사위를 돌리는 사건이 간단한 예시가 될 수 있습니다.
Unbiased Estimator
\(X_1, ..., X_n\)이 i.i.d.인 확률변수일 때, E(X)는 표본평균 \[\bar X=\frac{1}{n}\sum^n_{i=1}X_i\]
와 같습니다.
