Crossing the Reward Bridge: Expanding RL with Verifiable Rewards Across Diverse Domains

in Llm

Crossing the Reward Bridge: Expanding RL with Verifiable Rewards Across Diverse Domains
2025.03.31에 나온 논문이다.

abstract

  • 검증 가능 보상 강화학습(RLVR: Reinforcement Learning with Verifiable Rewards)은 수학, 코딩과 같은 구조화된 정답이 존재할 때 LLM의 성능을 효과적으로 향상시킴
    • but 덜 구조화된 real-world 도메인으로 확장하는 연구는 아직 부족하다.

-> 의학, 심리학, 경제학, 교육학 등 다양한 분야에서 구조화된 정답이 일반적으로 존재하지 않는 상황에서도 RLVR의 효과성과 확장 가능성을 탐구한다.

  1. 전문가가 작성한 정답이 있을 경우, 다양한 LLM들이 생성한 응답에 대한 이진(binary) 검증 판단(정답/오답)이 서로 높은 일관성을 보임

  2. 이진 판단의 한계를 극복하기 위해 soft rewards를 제공하는 generative scoring technique를 도입. 특히 자유형식이고 비구조적인 응답에서 더 유연하다.

    Motivated by this finding, we utilize a generative scoring technique that yields soft, model-based reward signals to overcome limitations posed by binary verifications, especially in free-form, unstructured answer scenarios.

-> 도메인별 데이터에 대해 광범위한 주석 없이도, 상대적으로 작은 크기(7B)의 LLM을 사용해 도메인 전반에 걸쳐 사용할 수 있는 보상 모델을 학습하는 것이 가능함을 실험을 통해 입증

-> 전반적인 실험 결과, 제안된 RLVR 프레임워크는 기존의 오픈소스 정렬(aligning) 모델인 Qwen2.5-72B 및 DeepSeek-R1-Distill-Qwen-32B보다 자유 형식 응답 환경에서 전반적인 성능을 크게 상회함을 입증 -> RLVR의 강건성(robustness), 유연성(flexibility), 확장성(scalability)을 크게 향상시키며, 이 분야에서의 중대한 발전을 나타낸다.

introduction

1. 전문가가 작성한 정답이 있을 경우, 다양한 LLM들이 생성한 응답에 대한 이진(binary) 검증 판단(정답/오답)이 서로 높은 일관성을 보임

고품질의 객관적인 참조(전문가가 작성한)가 주어졌을 때, 폐쇄형 모델(GPT-4o)이나 최근 공개된 고성능 오픈소스 모델(Qwen2.5-72B-Instruct) 등 다양한 LLM들 간에 이진 정답 판단의 일치도가 높다. 즉 이 발견은 참조 답안 기반 평가(reference-based evaluation)이 참조 없는 평가(reference-free verification)보다 상대적으로 더 쉽다는 것을 보여준다. 지금까지는 multi도메인 시나리오에서, 도메인별 대규모 정답 라벨링이 필요하다는 인식이 있었으나 이와 반대되는 새로운 보상 모델 학습의 방향을 제시한 것이다.

➡️ 대규모 수작업 라벨링이 필요 없다! 전문가가 작성한 정답(=reference)이 주어졌을 때, 다양한 LLM(GPT, Qwen 등)들이 생성한 응답에 대한 이진 판단의 일치도가 높다. 이 발견은 reference-based evaluation이 reference-free verification보다 상대적으로 더 쉽다는 것을 보여준다. 기존에는 extensive domain-specific annotation이 필요하다는 인식이 있었으나, 이 논문에서는 주석보다는 high-quality “objective reference”만 있으면 다양한 LLM들이 그걸 기준 삼아 서로 일치된 평가를 내릴 수 있다. ➡️ annotation 필요 없이 reference만 주면 된다

이진 보상은 지금까지 RLVR의 표준 방식이었지만, 비정형 과제에서는 분명한 한계를 보인다.

예를 들어, 실제 시험 문제 데이터를 분석한 결과:

  • 수학 문제 중 60.3%만이 규칙 기반 방법으로 검증 가능한 단일 숫자형 정답을 갖고 있으며,
  • 복잡한 다도메인 질문의 경우 그 비율은 45.4%로 더 낮아짐

2. 이진 판단의 한계를 극복하기 위해 soft rewards를 제공하는 generative scoring technique를 도입. 특히 자유형식이고 비구조적인 응답에서 더 유연하다.

이러한 한계를 해결하기 위해, 생성형 모델 기반 soft score를 RLVR에 직접 통합하는 방법을 제안한다.

we propose incorporating soft scores obtained from generative, model-based verifiers directly into RLVR

Specifically, we compute a soft reward from the probability of a single indicative token produced by a generative verifier summarizing its assessment.

we employ data composed of response samples and their corresponding judgments collected during RL exploration under the supervision of a larger cross-domain generative teacher model. These noisy yet more realistic datasets promote robustness of the subsequently distilled model-based rewards.

method

setting: 각 프롬프트 x에 대해 전문가가 작성한 참조 정답 a가 함께 주어지는 상황

모델의 응답 y와 실제 정답 a를 비교하여 검증하는게 이상적이지만, 실제 상황에서는 다음과 같은 문제가 영향을 줄 수 있다.

  • pattern-based verifier를 사용할 때 발생하는 불완전한 정답 추출 및 매칭
    • 패턴을 감지하지 못할 시에 발생할 수 있는 오류
  • 보상 모델 \(r_\phi(x, a, y)\)과 같이, 자동화된 평가 시스템에서 발생하는 노이즈
    • 보상 모델 \(r_\phi(x, a, y)\)란, LLM 기반 모델이 정답 여부를 판단
    • LLM이 틀리는 경우

그럼에도 불구하고, 연구진은 검증 가능한 보상을 사용하여 정책 그래디언트 기반 알고리즘을 적용한다. (verifiable reward in a policy gradient algorithm)

  • 검증 가능한 보상: 정답 여부를 판별할 수 있는 경우 (정답이 주어진 경우)
  • 정책 그래디언트 기반 알고리즘: 모델(=policy)이 어떤 행동을 했을 때 받은 보상을 이용해, 앞으로도 이런 행동을 더 자주 하도록 파라미터를 조정하는 것

이를 식으로 표현하면 다음과 같다.

❗️ [expected reward] 모델의 기대 보상 수식

\(J(\theta)=\mathbb{E}_{(x, a) \sim D} \mathbb{E}_{y_i \sim \pi_\theta(\cdot \mid x)}\left[r_\phi\left(x, a, y_i\right)\right]\) -> 현재 모델이 만들어내는 응답들이 얼마나 좋은지를 평균적으로 계산하는 식이다. 즉, 모델이 지금 상태로 얼마나 성능이 좋은지를 수치로 나타내는 함수이고, 강화학습에서는 이 값을 최대화하는 방향으로 학습한다.

  • \[\theta\]
    • 모델의 파라미터(현재 모델의 weight 값들)
  • \[(x, a) \sim D\]
    • 데이터셋 D에서 프롬프트 x와 참조 정답 a를 샘플링한다.
    • 학습에 사용할 문제-정답 쌍을 하나 고르는 과정
  • \[y \sim \pi_\theta(\cdot \mid x)\]
    • 현재 모델 \(\pi_\theta\)가 프롬프트 x를 보고 응답 y를 생성하는 과정
  • \[r_\phi\left(x, a, y_i\right)\]
    • 보상 함수
    • 입력 x, 참조 a, 모델 응답 y를 받아서 이 응답이 얼마나 잘했는지를 점수로 반환한다.
    • 이때 이진 보상이면 정답 1, 오답 0
    • soft reward이면 정답에 가까우면 0.9: 연속형 점수

모든 프롬프트/정답 쌍에 대해, 모델이 생성할 수 있는 모든 응답 y를 샘플링해서 각각이 받는 보상 \(r_\phi\)를 계산해보고, 그걸 평균 내면, 현재 모델의 전체적인 성능 \(J(\theta)\)가 나온다.

이 기대 보상을 최대화 하는 방향으로 모델을 업데이트 한다.

❗️ [gradient] 모델 업데이트 수식

위의 기대 보상 수식을 미분한 식이다. 즉, 어느 방향으로 파라미터를 바꾸면 보상이 올라갈지 계산하는 식이다. \[\nabla_\theta J(\theta)=\mathbb{E}_{(x, a) \sim D} \mathbb{E}_{y_i \sim \pi_\theta(\cdot \mid x)}\left[r_\phi\left(x, a, y_i\right) \nabla_\theta \log \pi_\theta\left(y_i \mid x\right)\right]\]

\(\nabla_\theta \log \pi_\theta\left(y_i \mid x\right)\): 응답 y를 더 잘 생성하려면 모델 파라미터를 어떻게 바꿔야 할지를 알려준다. 점수가 낮으면 파라미터를 줄이고, 점수가 높으면 파라미터를 그쪽으로 강화하는 식이다. \(\pi_\theta\left(y_i \mid x\right)\): 프롬프트 x에 대해 모델이 응답 y를 낼 확률 \(\log \pi_\theta\left(y_i \mid x\right)\): 그 확률의 로그 \(\nabla_\theta\): 이 로그 확률을 모델 파라미터 \(\theta\)에 대해 미분한 것

보상함수 r: 완벽한 정답일 시에 1.0, 틀린 답일 시에 0.0의 값을 가질 것이다. 그러면 \(r ⋅ \nabla_\theta \log \pi_\theta\left(y_i \mid x\right)\) 에서 틀린 답은 전체 항이 0이 될 것이고, 정답은 전체 항이 크게 남아서 응답 A가 생성될 확률을 더 높이기 위한 파라미터 방향으로 조정된다.

3.1 Reward Estimation

👾 이 논문에서는 생성형 LLM \(\pi_\phi\)로 이진 보상 신호를 자동 생성한다. 이 \(\pi_\phi\)를 검증기(verifier)라고 부른다.

프롬프트는 다음과 같다.

각 응답이 정확히 T개의 단계(step)로 구성된다고 가정했을 때, 응답 \(y_i\)의 마지막 단계는 \(y_i^T\)로 표기한다. 이진 보상함수는 다음과 같이 정의된다. \[r_\phi(x, a, y_i) = c_i = 1\]

여기서 \(c_i\)는 \(y_i\)가 정답과 일치하는지에 대한 \(\pi_\phi\)의 판단이다. 즉 0 또는 1의 값이 들어간다.

이 검증기로서의 \(\pi_phi\)를 사용하여, 판단 토큰 (0 또는 1)의 확률을 이용해 soft reward 함수도 정의할 수 있다. \[r_\phi(x, a, y_i) = \begin{cases} \pi_\phi(1 \mid x, a, y^T_i) & \text{if } c_i = 1 \\ 1 - \pi_\phi(0 \mid x, a, y^T_i) & \text{if } c_i = 0 \\ 0 & \text{otherwise} \end{cases}\]

이렇게 정의된 soft reward 함수 \(r_\phi(x, a, y_i)\)는 항상 [0,1] 범위 안에 있으므로, 기존의 이진 보상 기준과 호환된다.

3.2 Reward Normalization

안정적인 gradient(기울기) 계산과, 배치 내 평균 이상 성능을 보인 샘플의 개선을 유도하기 위해, 보상에 대해 z-score normalization을 적용한다.

정규화된 보상은 다음과 같이 계산된다. \(\tilde{r}(x, a, y_i) = \frac{r(x, a, y_i) - \mu_r}{\sigma_r}\)

\(\mu_r\): 해당 배치 내 모든 샘플의 평균 보상 \(\sigma_r\): 표준 편차

모든 샘플의 보상이 동일할 때 \(\sigma_r = 0\)인데, 이때는 정규화된 보상을 0으로 설정한다. 현재 정책에게 너무 쉽거나 어려운 샘플일 수 있어 학습 효과가 없다고 판단하는 것이다.

3.3 Reward Model Training

일반적으로는, 이미 학습이 잘 되어 있고 판단도 꽤 정확한, 정렬된 LLM(aligned LLM, 예: GPT-4, Qwen2.5-72B-Instruct)을 judge로 그대로 쓴다. 하지만 이 논문에서는 그런 LLM은 너무 크고, 도메인 간 일관성과 성능이 불안정하다고 말한다.

  • 72B 모델은 62.7% 정확도
  • 7B 모델은 58.8% 정확도 작은 모델은 빠르고 가볍지만, 성능이 생각보다 많이 떨어질 수 있다.

➡️ 적당한 크기의 보상 모델을 범용 도메인용으로 직접 학습시킨다.

정답 보상 레이블이 없는 상황에서, 각 \((x, a, y)\)에 대해, 고정된 LLM을 프롬프트로 사용해 이진 판단 \(c \in {0,1}\)를 얻는다.

여기서 고정된 LLM이란 학습되지 않고 그대로 사용하는 언어모델이다.

그렇게 수집된 \((x,a,y,c)\) 데이터를 활용해, 보상 모델을 지도학습 방식으로 학습한다. 이렇게 학습된 보상 모델의 출력으로 soft reward \(r_\phi(x,a,y)\)를 계산해서 REINFORCE 등의 알고리즘으로 actor 모델을 강화학습시킨다.

큰 cross-domain teacher 모델의 감독 아래에서 RL 탐색 중 수집한 응답 샘플과 판단 데이터를 활용 (Instead, we employ data composed of response samples and their corresponding judgments collected during RL exploration under the supervision of a larger cross-domain generative teacher model.)

이때 응답 y는 고정된 모델이 아니라 점점 개선되는 actor policy로부터 생성되기 때문에 다양한 품질과 포맷의 노이즈가 섞인 응답이 존재한다. 하지만 이 점이 오히려 보상 모델의 robustness를 높이는 데 기여할 수 있다고 한다.

implementation details

reward 업데이트 방법

Qwen2.5-72B-Instruct에서 추출한 16만개의 distilled 데이터를 얻은 후, 이 데이터를 활용해 Qwen2.5-7B-Instruct 모델에 대해 지도학습을 수행했고, 그 결과로 reward 모델을 만들었다. ➡️ 72B 모델로 판단한 결과를 7B 모델에 옮기는 과정이다. 연구진은 제안한 방법의 효과를 검증하기 위해 REINFORCE, RLOO, REINFORCE++와 같은 여러 강화학습 알고리즘을 사용했다. 기존 연구를 따라, 보상 모델의 편향을 완화하기 위해 강화학습 모델과 base model의 분포 간에 KL divergence 패널티를 추가했다. ➡️ 초기 모델과 너무 멀어지지 않게 잡아주는 패널티이다. \[\tilde{r}(x, a, y_i) \leftarrow \tilde{r}(x, a, y_i) - \beta \log \frac{\pi_\theta(y_i \mid x)}{\pi_{\text{ref}}(y_i \mid x)}\]

\(\tilde{r}(x, a, y_i)\): 원래 계산된 soft reward \(\pi_\theta\): 현재 actor(policy) 모델의 출력 분포 \(\pi_{\text{ref}}\): base 모델의 출력 분포 \(\beta\): KL 패널티의 강도

논문에서, 모든 실험에서 \(\beta\)는 0.01로 설정되었다.

evaluation

Qwen2.5-72B의 다수결 기반 이진분류와 GPT-4o의 단일평가 간의 실험을 진행했다. Qwen2.5-72B는 m개의 판단 중 절반 이상이 정답이라고 분류한 경우 올바른 응답(1)의 결과를 냈고, GPT-4o의 단일 평가와 일치도를 Cohen’s Kappa 계수를 이용해 측정했을 때

  • 수학 문제에서는 \(\kappa > 0.86\)
  • multi subject 문제에서는 \(\kappa > 0.88\) 로, 거의 완벽한 일치도를 보였다. 이 높은 일치도는 다양한 m값에 대해서 일관되게 유지되었으며, 결과가 m의 크기에 크게 민감하지 않음을 시사한다. 이 실험 결과에 따라 이후 모든 실험에서는 m=1(단일 판단)으로 설정하여 효율성을 높이면서도 평가 품질을 유지했다.

최종 정리

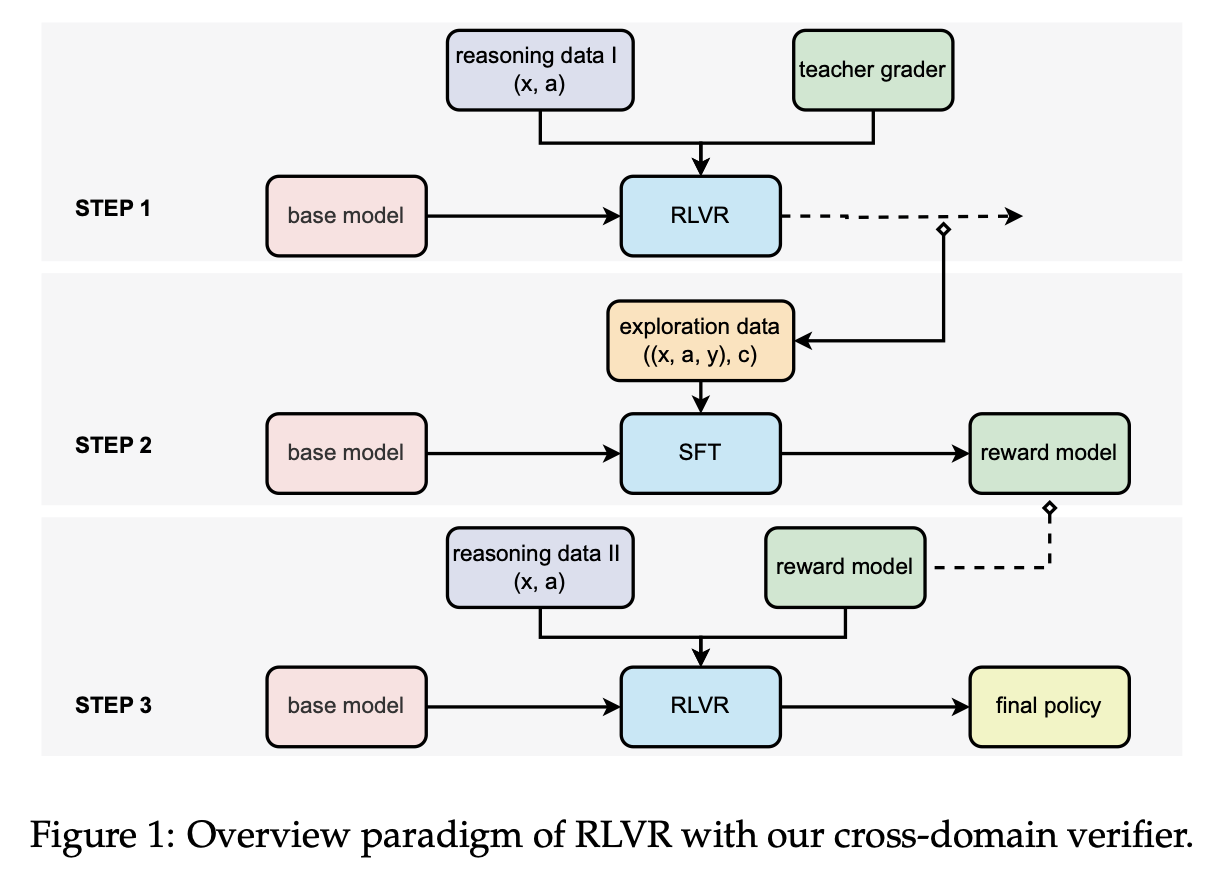
step1. 라벨 수집

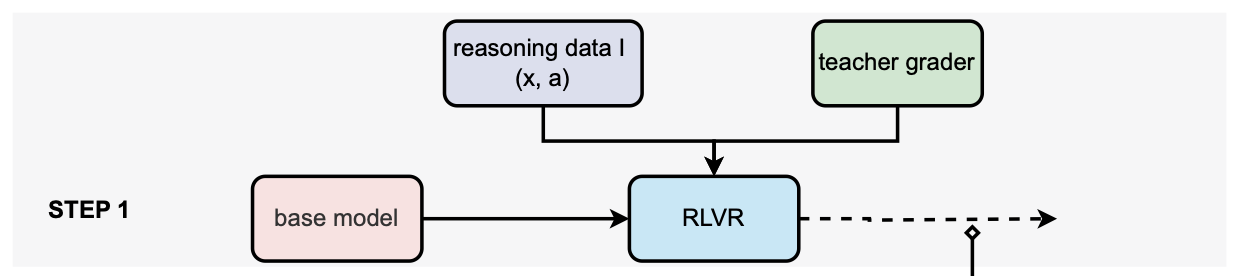exploration의 단계이다.

  1. 데이터 (x,a)를 고정된 상태(학습 전 초기 상태)의 base model에 넣고 응답 y를 생성한다.
  2. teacher grader, 즉 크기가 큰 LLM을 통해 정답여부에 대한 이진 라벨 \(c\)를 얻는다. teacher grader가 보상을 주는 형태이기 때문에, 응답 생성은 강화학습 방식과 유사한 구조이지만 정책 업데이트는 일어나지 않는다. ➡️ \((x,a,y,c)\)

step2. 보상 모델 학습

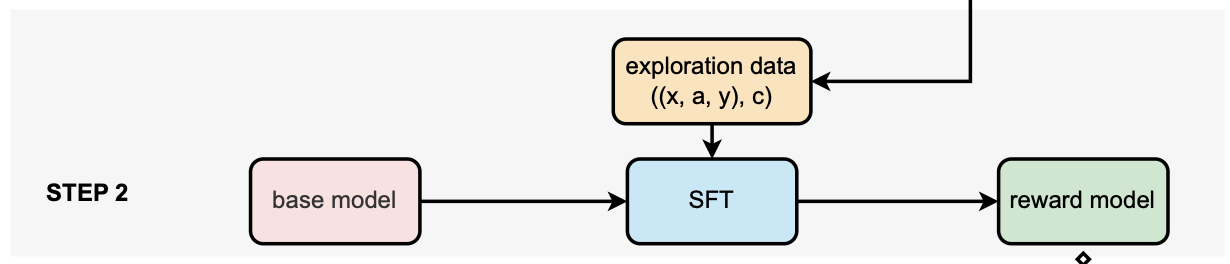즉, reward 모델을 만드는 과정이다. 위에서 얻은 \((x,a,y,c)\)를 base model에 주고, SFT 방식으로 학습시킨다. 이를 통해 학습된 reward 모델을 얻을 수 있다. ➡️ reward 모델 \(r_\phi(x,a,y)\)

step3. 최종 강화학습

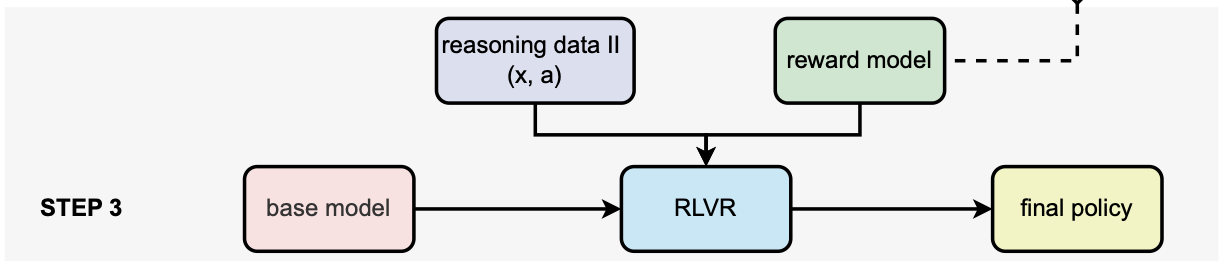데이터 (x,a)를 base모델에 넣고 응답을 생성하며, step2에서 학습된 reward 모델이 보상을 준다. policy gradient를 진행하며 강화학습이 이루어지고, 최종 final policy가 완성된다! ➡️ final policy

result

  • 제안된 RLVR 프레임워크가 다양한 도메인에서 매우 효과적임을 확인
  • 7B 크기의 베이스 모델을 여러 RL 알고리즘과 함께, 논문의 soft reward 검증기로 미세조정한 결과, Qwen2.5-72B-Instruct나 DeepSeek-R1-Distill-Qwen-32B 같은 최신 오픈소스 정렬 모델보다 최대 8.0% 정확도 향상을 달성
  • 특히, 비정형 응답 시나리오나 더 큰 훈련 데이터 환경에서, 논문의 모델 기반 soft reward가 기존 이진 보상보다 더 잘 확장되고, 더 강건한 정책(policy)을 생성함을 확인 ➡️ multi domian에서 효과적임

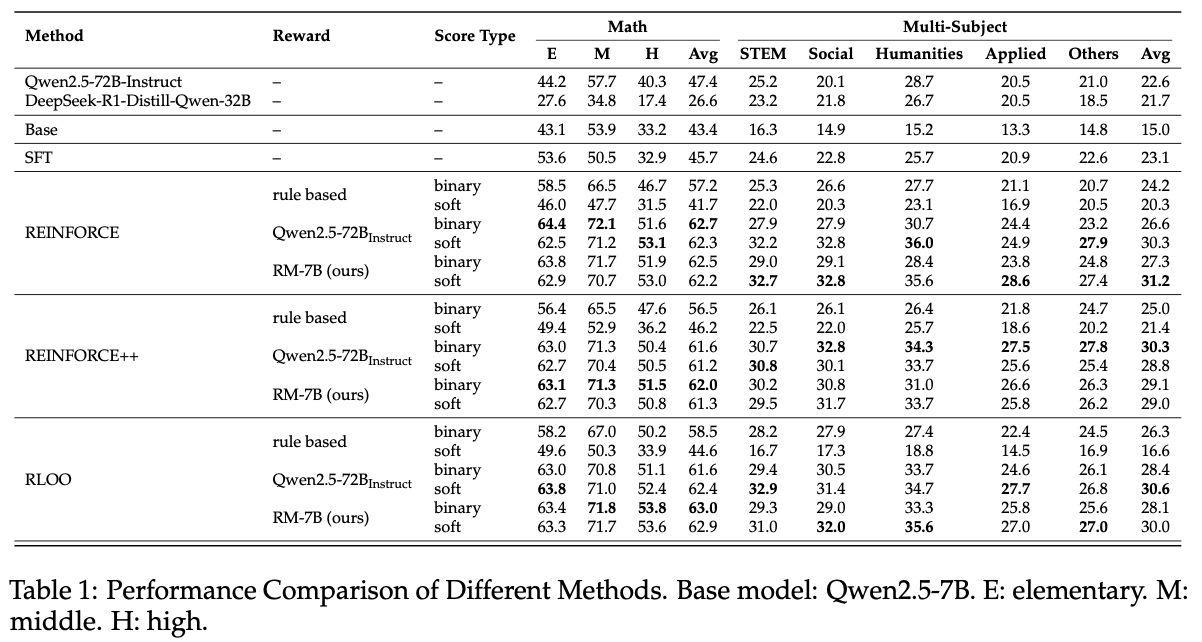
수학 및 multi-subject 과제에 대한 결과를 나타낸 표이다.

  1. base 모델 평가 결과 본 연구에서 사용한 데이터는 난이도가 상당히 높으며, Qwen2.5-72B-Instruct나 DeepSeek-R1-Distill-Qwen-32B 같은 고성능 오픈소스 모델조차도 만족스러운 성능을 내지 못했다.
  2. SFT vs. RL 수학과 multi-subject 과제 모두에서 SFT는 RL에 비해 성능이 크게 떨어진다.
  3. Model-based reward vs. Rule-based reward 자유형식 응답 조건에서, 모델 기반 보상은 규칙 기반 보상보다 항상 좋은 성능을 보였다.

    RLOO 기준 RM-7B: 63% Qwen-2.5-72b-Instruct(binary reward): 61.6% rule-based: 58.5%

참고로 rule-based는 정해진 패턴에 따라 정답을 판단하는 식이고 model-based는 모델이 판단하는거라 더 유연하다. 특히 논문의 모델 RM-7B는 더 큰 Qwen모델보다도 높은 정확도를 기록했다.

  1. Binary reward vs. Soft reward
    • rule-based rewards에서는 soft reward가 binary reward보다 성능이 낮았다. 그 이유는 answer과 reference 사이에 중복되는 토큰 때문에 soft score가 낮아졌을 수 있다. 문장 임베딩 간 코사인 유사도 같은 보상이 더 나은 대안이 될 수 있다.

  • 반면, model-based rewards에서는 수학 문제에서 soft/binary의 성능 차이가 크게 없었다. 수학 문제는 정답 판단이 상대적으로 쉬워서, 모델이 판단에 대해 확신이 높기 때문으로 보인다.

  • 그러나 multi-subject 과제에서는, 참조 정답이 더 다양하고 판단이 복잡하기 때문에, soft reward가 더 신중하게 판단하고, 때때로 binary reward보다 좋은 성능을 냈다.

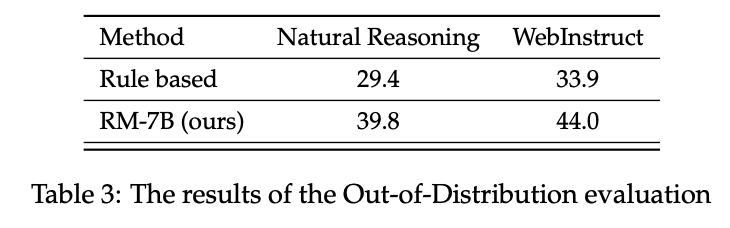
➡️** RLVR 분야에서 SOTA를 달성했다.**

  1. model-based > rule-based
  2. Qwen2.5-75B에서 추출한 데이터로 더 작지만 효율적인 RM-7B 모델을 학습해 동등하거나 더 좋은 성능을 냄
  3. binary reward를 soft reward로 확장하여, 참조 정답이 다양한 과제에서도 더 신중하고 유연한 평가를 가능하게 함

결론

대규모 수작업 라벨링 없이도 보상 모델을 학습할 수 있다. RL 과정 중 모델이 생성한 응답들을 활용해서 자동으로 라벨을 수집하고, 그걸로 보상 모델을 학습

  • 강화학습 원래 있던 것들 조합해서 쓴거
    • 데이터셋을 더 신경써서 만들수있지 않았나?
    • step1 -> step2 -> step3 세 단계로 가는게 아니라
    • (step1 - step2 - step3)를 한 단계로 iteration 돌리면 더 성능이 좋은 데이터셋을 만들 수 있었을 것
    • KL divergence를 쓰는게 base model에서 멀어지지 않게 함인데 …
    • step1에서 학습해둔게 step3 KL divergence를 넣으면서 성능 떨어뜨리는 느낌?
    • 근데 강화학습에서 다 그렇게 한다고 함 (세 단계)
  • 여러 도메인에 먹혔다 <- 이게 핵심