Model-based Collaborative Filtering
Model-based Collaborative Filtering
Model-based CF는 머신러닝을 더욱 적극적으로 사용하는 추천 알고리즘입니다. 이전까지는 유사도를 기반으로 추천했다면, model-based는 데이터의 패턴을 학습합니다. 데이터의 패턴을 학습한다는 것은, 데이터(유저)의 특성을 추출해야 함을 의미합니다. 이를 활용하여 model-based CF는 유저의 잠재적 특성을 파악해 냅니다.
Model-based CF의 핵심 개념으로는 크게 세 가지가 쓰입니다. 1) Latent Factor 2) Matrix Factorization 2-1) Singular Value Decomposition
미리 요약하자면, 1번 Latent Factor는 유저와 아이템 간의 관계를 구성하는 잠재적인 요인이고, 2번 Matrix Factorization은 이를 구현하는 방법으로, 행렬 분해를 뜻합니다. 2-1번 Singular Value Decomposition은 행렬을 분해하는 방법 중 하나입니다.
Latent Factor
Latent Factor는 말 그대로 잠재적인 요인입니다. Latent Factor Model은 유저와 아이템 간의 관계를 각각 Latent Vector로 학습하게 됩니다. 이 요인을 찾아냄으로써 우리는** User-Item 행렬에서 각각을 factor로 나타낼 수 있고, 그 결과 User과 Item을 같은 vector space에 represent할 수 있습니다.** 그러면 우리는 같은 공간에서 어떤 User와 어떤 Item이 비슷한지를 확인할 수 있습니다.
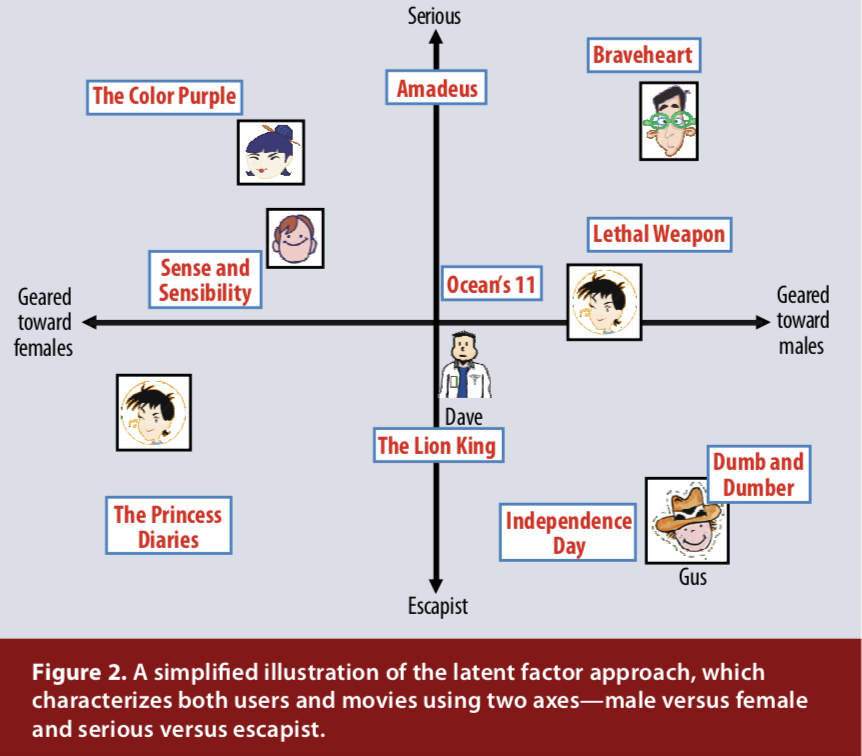
위의 그림과 같은 벡터 공간이 표현되면, 사용자와 아이템이 가까우면 유사하고 멀리 떨어져 있으면 유사하지 않다고 판단할 수 있겠습니다.
제가 이해한 바로는, 사용자에게 아이템을 추천해주는 과정에서 어떤 특성을 추천의 기준으로 활용해야 하는가 - 에서 이 “특성”이 Latent Factor가 되는 것이라고 이해했으며, 이 잠재 요인이 무엇이 될지는 정확히 알 수가 없고 정해진 값이 아닙니다.
Matrix Factorization
다음 그림의 우측 하단에 User-Item Matrix가 있습니다. 이 행렬 데이터를 이용해 Collaborative Filtering 모델이 차원 축소 과정에서 잠재 요인을 찾아냅니다. 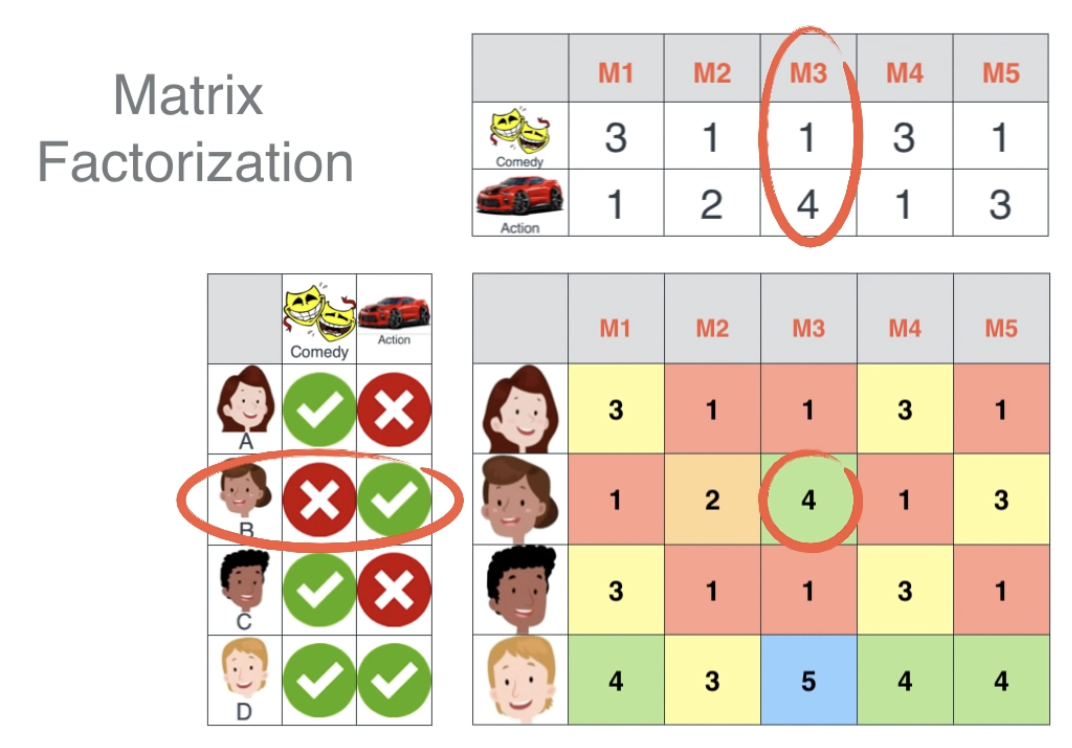
User-Item Matrix(사용자-아이템 행렬)에서 “장르”라는 잠재 요인을 찾아내면, ‘사용자-아이템’ 행렬을 ‘사용자-장르’, ‘장르-아이템’ 2개의 행렬로 분해할 수 있습니다.
이 분해 작업이 바로 Matrix Factorization입니다.
이와 같이 Latent Factor는 행렬 분해(Matrix Factorization)를 통해 얻어질 수 있습니다. Matrix Factorization을 일반화하면 아래의 그림과 같이 나타낼 수 있습니다.
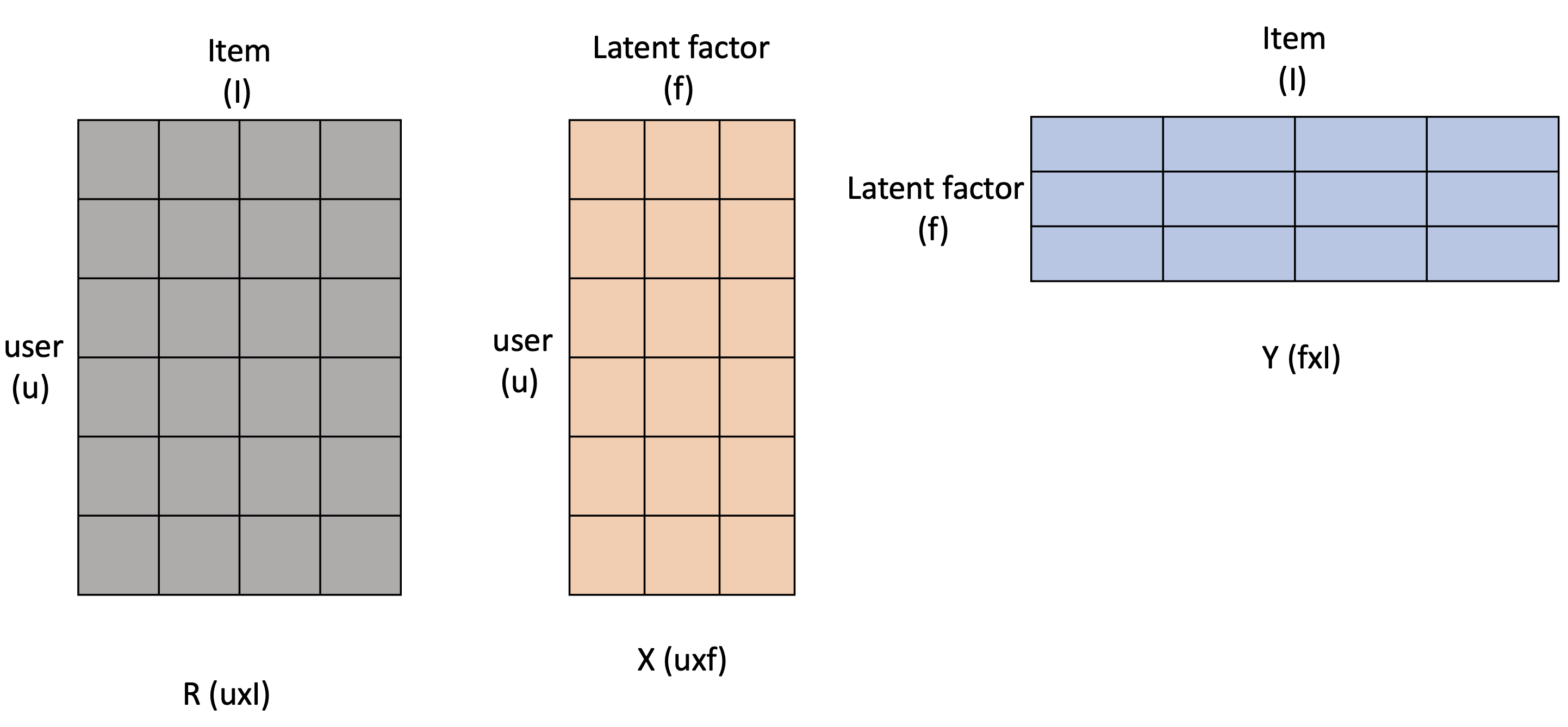
(출처: https://velog.io/@hyxxnii/Ch-06-3.-Latent-Factor-Model-Matrix-Factorization)
사용자-아이템 행렬을 Rating Matrix라고 부르며, 보통 R로 표현합니다. shape는 User의 수 * Item의 수 입니다. X는 User의 latent factor matrix (shape: U * f), Y는 Item의 latent factor matrix (shape: f * I) 입니다.
여기서 f가 나오는데요, f는 임의의 dimension을 뜻합니다. 보통 행렬 분해는 차원 축소를 하기 위해 수행되죠. 우리는 R 행렬의 차원을 f차원으로 줄여주고 있는 것이고, 이 값은 우리가 직접 정해줍니다.
Rating Matrix는 당연하게도 모두 채워져 있지는 않을 것입니다. User가 Item을 얼마나 선호하는지 다 알고 있으면 추천할 게 없으니까요. 예를 들면 User B가 아직 시청하지 않은 영화 Item C의 칸은 비워져 있을 것이고, 이 빈칸을 예측하는 것이 모델의 기본 원리입니다.
관측된 데이터만 채워져 있는 행렬에서 빈칸을 채우면 예측된 Rating Matrix(\(\hat r_{ui}\))를 얻을 수 있습니다. \(X^T\)와 \(Y\)의 내적 곱(inner product)을 사용하여 계산합니다. \(\hat r_{ui} = X^T_u*Y_i\)
정답인 Rating matrix와 예측된 Rating matrix가 유사하도록, 즉 오차가 최소화되도록 모델을 학습합니다.
Singular Value Decomposition
행렬 분해를 해야하는 건 알겠는데, 이걸 어떻게 분해하는 걸까요? 이때 대표적으로 사용되는 기법이 Singular Value Decomposition(SVD, 특이값 분해)입니다. 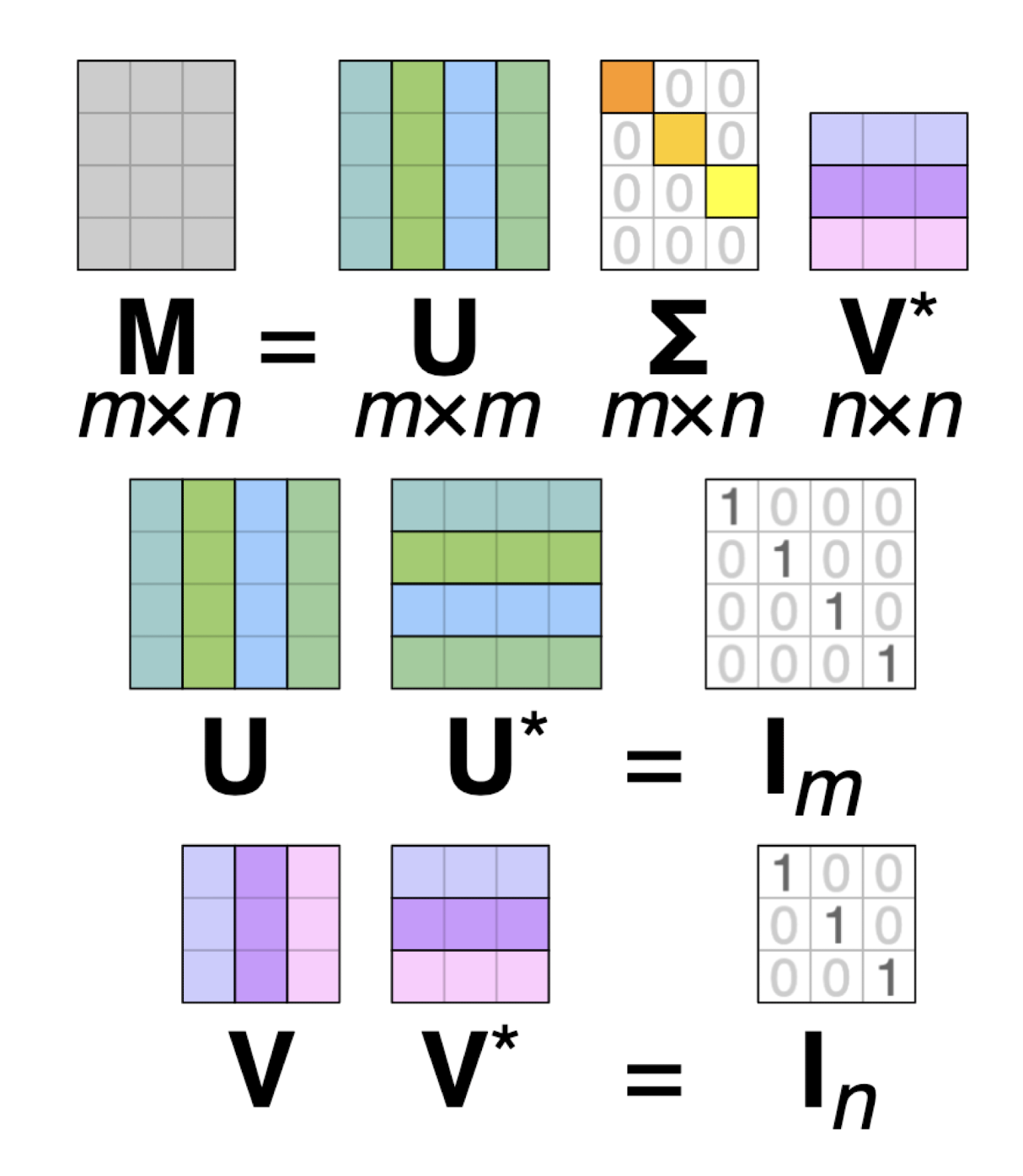
행렬 M은 다음과 같이 분해될 수 있습니다. \(M=U \sum V^T\)
- \(U(m*m)\)와 \(V(n*n)\)는 orthogonal matrix
- \(\sum(m*n)\)은 diagonal matrix
- 대각원소는 eigen value의 제곱근으로, A의 특이값입니다.
구체적인 내용은 선형대수학을 참고하시면 좋을 것 같습니다.
최종적으로, Model-based Collaborative Filtering의 추천시스템 알고리즘 수행 과정은 다음과 같이 표현할 수 있겠습니다. 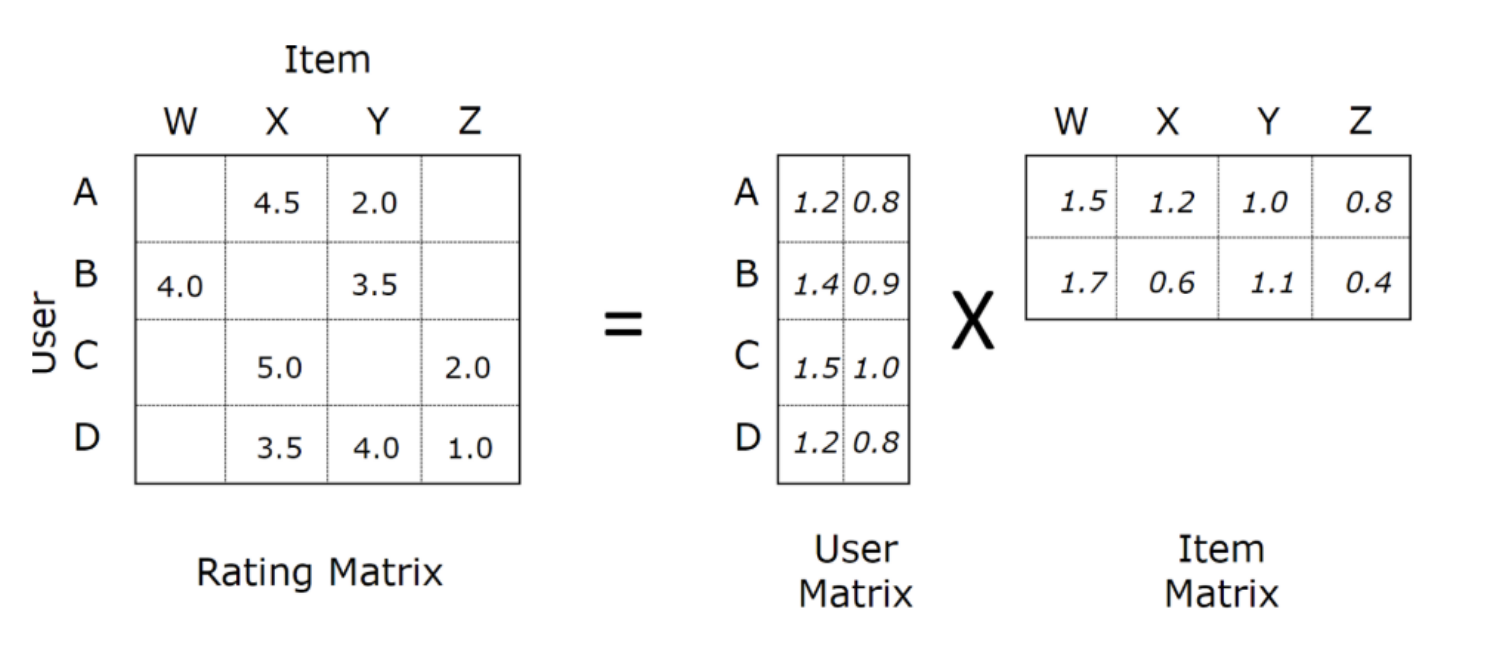
Loss Function of Matrix Factorization
Loss Function(손실함수)은 모델이 얼마나 ‘못’ 예측하는지를 확인하기 위한 평가지표로 사용되는 함수입니다. Loss function: \(min∑_{(u,i)∈T}(r_{ui}−x^T_uy_i)^2+λ(‖x_u‖^2+‖y_i‖^2)\)
- \(x_u, y_i\) : User와 Item latent vector
- \(r_{ui}\) : User u가 Item i에 부여한 REAL rating
- \(\hat r_{ui} = x^T_uy_i\) : User u가 Item i에 부여한 PREDICTED rating
- \(λ(‖x_u‖^2+‖y_i‖^2)\) : overfitting 방지를 위한 penalty(regularization) term
실제 rating에서 예측 rating을 빼서 제곱오차를 구하는 Loss Function으로, 그 오차를 최소화할수록 실제 값과 예측 값이 유사해질 것입니다.
Optimization of Matrix Factorization
위의 손실함수를 어떻게 최소화할 수 있는가를 다루는 최적화 알고리즘입니다.
1. SGD(Stochastic Gradient Descent)
경사하강법이라고 불리는 기법이기도 합니다. SGD는 Error term을 줄여나가는 방식으로 \(x_u\)와 \(y_i\)를 update합니다. Error term은 실제 평점과 예측 평점의 차이를 error term으로 정의합니다.
Error term \(e_{ui} = r_{ui}-X^T_iy_u\) 현재에서 gradient의 반대 방향으로 \(x_u\)와 \(y_i\)를 업데이트합니다. 그 다음 \(x_u\)를 구할 때 이전 값보다 더 작아졌다면 그 방향으로 움직이면 됩니다.
Updating Equation \(x_u←x_u+γ(e_{ui}⋅y_i−λ⋅x_u)\) \(y_i←y_i+γ(e_{ui}⋅x_u−λ⋅y_i)\)
2. ALS(Alternating Least Squares)
대부분의 경우, \(x_u\)와 \(y_i\)를 둘 다 알 수 없기 때문에 풀어야 하는 문제는 non-convex합니다. 
ALS는 이를 풀기 위해 \(x_u\)와 \(y_i\)를 교대로 하나는 고정하고, 하나는 update해가는 방식으로 문제를 풀어나가는 방법입니다. \(x_u\)와 \(y_i\)는 독립적으로 계산되기 때문에, 병렬적으로 처리할 수 있습니다.
Explicit/Implicit Feedback
모델을 학습시키는 데이터는 Explicit Feedback, Implicit Feedback으로 나눌 수 있습니다. 각 데이터의 특징은 다음과 같습니다. 
참고: https://seunghan96.github.io/rs/4.Model-based-Collaborative-Filtering/
