Intro
Introduction
 (출처: AAA/Fast Campus)
(출처: AAA/Fast Campus)
What is Recommender System?
정보 필터링 기술의 일종으로, 어떤 대상에게 어떤 아이템을 데이터 기반으로 추천해주는 알고리즘입니다. 현업에서는 RecSys라는 분야로 구분되고는 합니다.
RecSys의 구성요소
User & Item으로 구분됩니다.
- 특정 User에게 “적합한 Item” 추천해주기
- 해당 Item을 좋아할 “적합한 User” 추천해주기
User 요소에는 사용자 고유의 정보(성별, 나이 등)와 사용자의 로그 정보(이용 시간, 이용 컨텐츠 등)가 입력될 것이고, Item 요소에는 컨텐츠 고유의 정보(출시연도, 장르 등)가 입력될 것입니다.
RecSys의 score
추천을 진행할때 사용하는 점수로, User와 Item이 얼마나 적합한지를 점수화하는 작업을 통해 얻어집니다. 알고리즘별로 점수화 방법은 다르며, 보통 벡터화 작업으로 수행되고는 합니다. 추천 점수를 잘 점수화(Scoring)하는 알고리즘이 좋은 추천 알고리즘이라고 할 수 있습니다.
RecSys의 Task
- 랭킹 문제
- User가 특정 Item을 선호할지 안할지 (정확한 점수 파악은 하지 않습니다.)
- TOP5 User/Item
- 예측 문제
- User가 특정 Item을 얼마나 선호할지 (=score)
- User x Item Matrix
- 채워져 있는 값: model training을 위한 값
- 비워져 있는 값: model testing을 위한 값
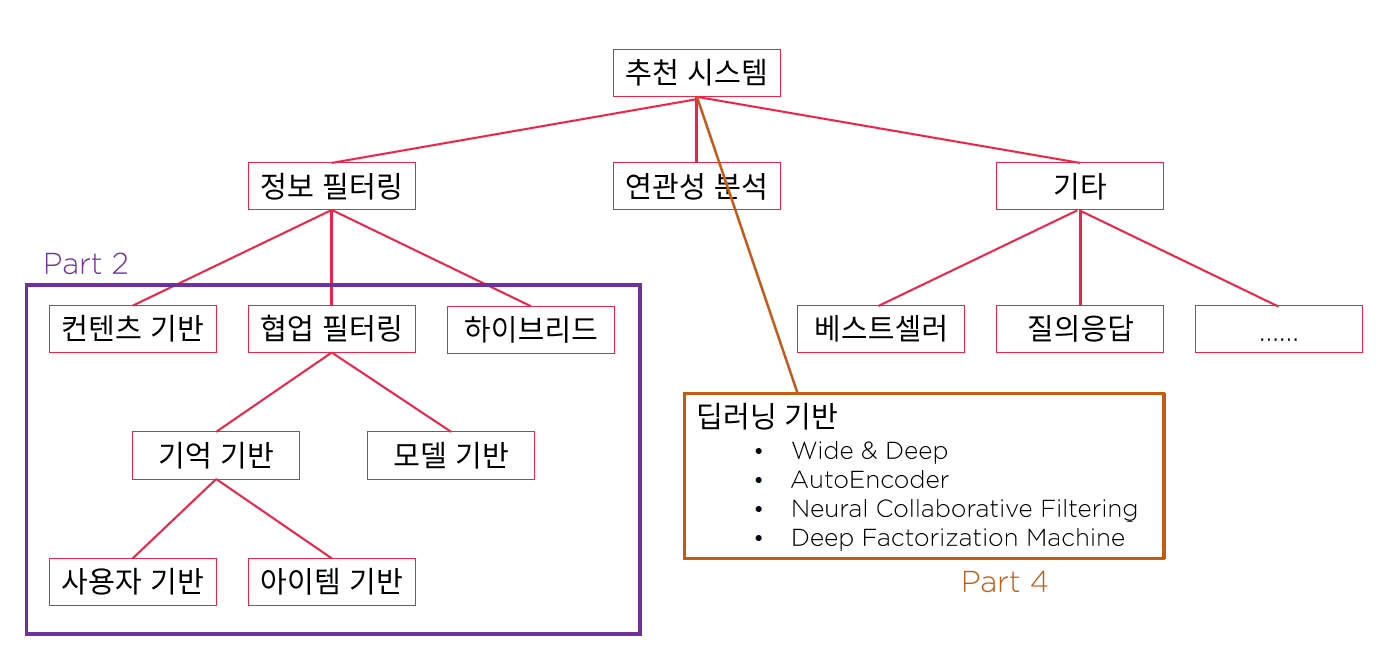
추천 알고리즘의 종류
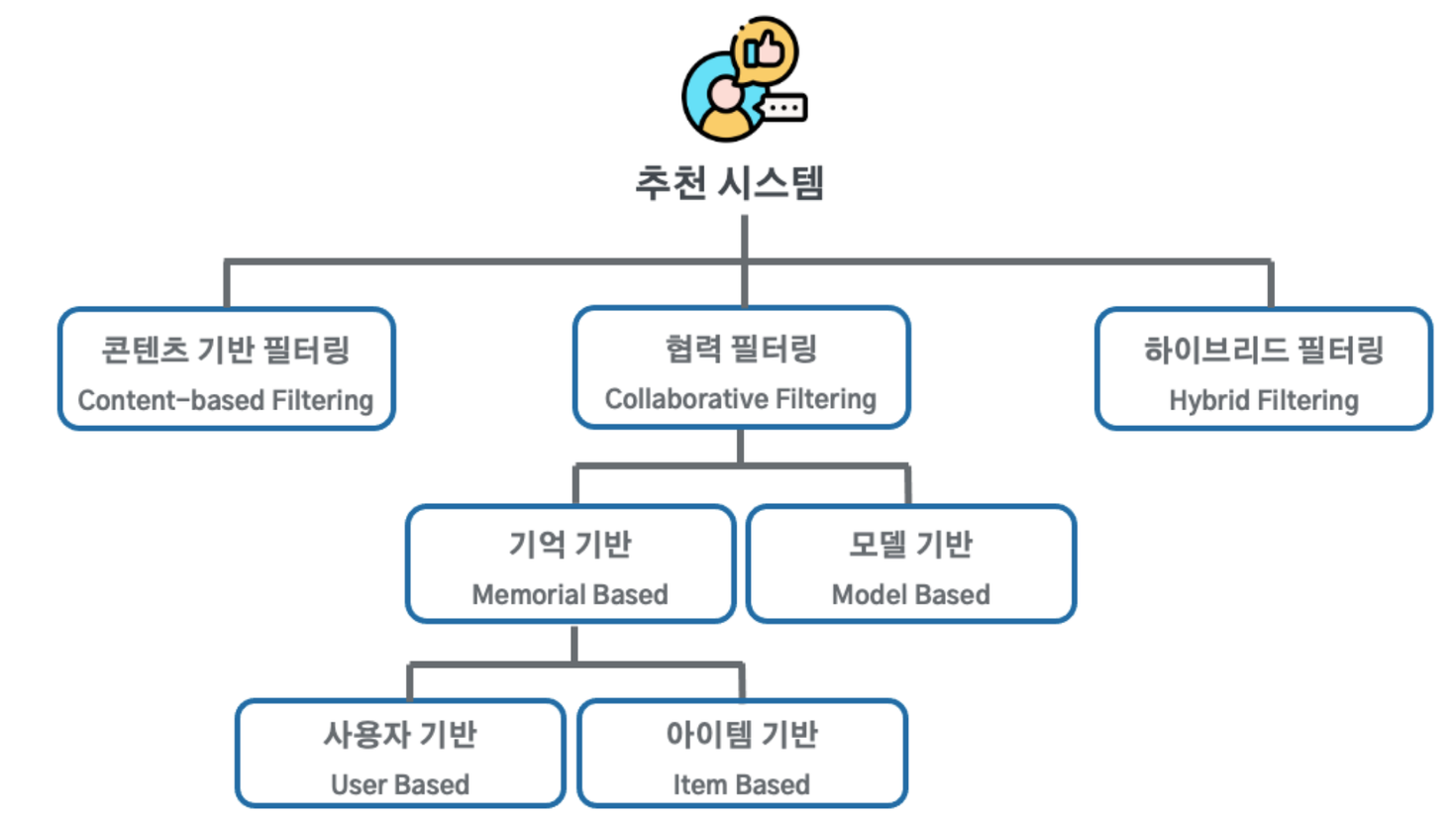
Content-based Filtering
User의 과거 이력을 기반으로 유사한 Item을 추천해주는 방식입니다. User의 과거 로그 정보 외에도 Item의 기본 정보가 필요할 것입니다. 해당 Item을 설명할 수 있는 특징을 모델이 이해할 수 있는 형태인 벡터로 바꿔주는 벡터화 작업이 수행되어야 합니다.
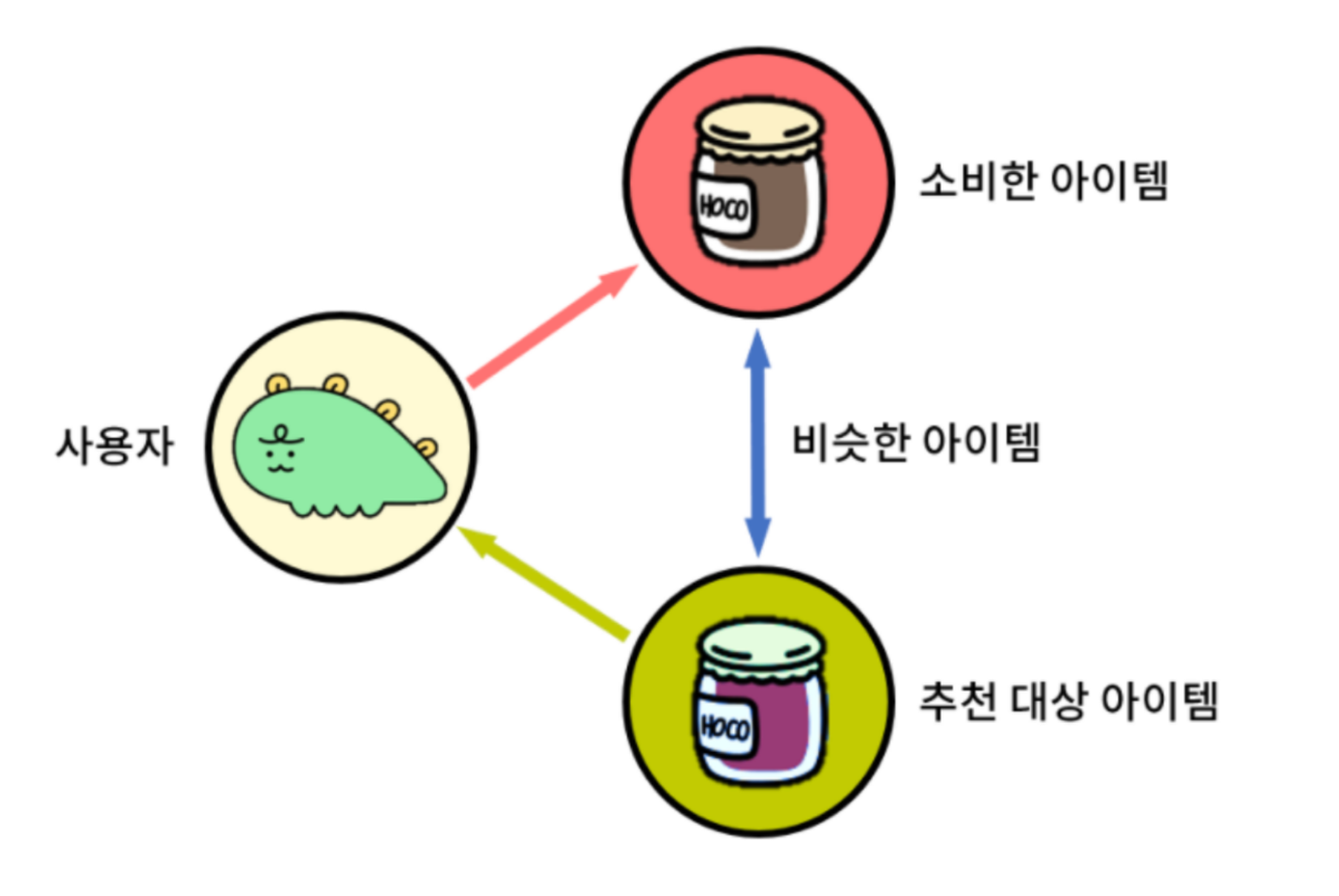
한계: Item의 기본 정보만을 활용해야 하기 때문에, 비슷한 분류만 계속해서 추천하게 됩니다. 다양한 형식의 항목 추천이 어렵습니다.
Collaborative Filtering
User의 정보를 기반으로 비슷한 성향을 가진 다른 User가 좋아하는 Item을 추천해주는 방식입니다. 이를 위해 많은 사용자로부터 수집한 구매 패턴이나 평점 데이터를 사용해야 합니다. A와 B가 유사한 장르의 시청 기록을 가지고 있으면, A가 본 영화를 B에게 추천해줄 것입니다.
한계: Cold Start, 많은 연산량, Long tail Cold Start 현상은 모델이 충분한 데이터가 수집된 상태가 아니라서 추천을 진행해주지 못하는 상태를 칭합니다. Long Tail 현상은 콘텐츠 추천이 비대칭적으로 이루어지는 현상을 뜻하는데, 인기 있는 소수의 콘텐츠만을 주로 추천하게 되어 추천의 다양성이 떨어지는 문제가 발생합니다.
Hybrid Filtering
Content-based Filtering + Collaborative Filtering 이 조합 외에도 2가지 이상 다양한 종류의 추천 시스템 알고리즘을 조합하는 방법을 모두 Hybrid Filtering이라고 부릅니다.
RecSys의 한계
- Scalability 실제 데이터는 학습/분석에 사용한 데이터보다 다양하고 많습니다.
- Proactive RecSys 이론에서는 유저의 행동/정보 제공 이후에 추천이 진행되는데, 실제로는 특별한 요청 없이 사전에 먼저 제공해야 경쟁력 있는 서비스가 됩니다.
- Cold-Start
RecSys의 유사도
추천시스템은 기본적으로 Item간의 유사도, User간의 유사도를 계산해야 합니다. 유사한 취향을 가진 사용자가 누구인지, 유사한 아이템으로 어떤 것을 추천해주어야 하는지 알아야 하기 때문입니다. 이때 사용되는 다양한 유사도 지표가 있습니다.
Euclidean Distance
두 개의 실수값을 갖는 벡터간의 평면 위에서의 거리를 계산합니다. \(x=(x_1, x_2, ..., x_n)\)과 \(y=(y_1, y_2, ..., y_n)\)의 유클리디안 거리 \(\bar{xy}\)를 구합니다. \[\begin{array}{l} \sqrt{\left(a_{1}-b_{1}\right)^{2}+\left(a_{2}-b_{2}\right)^{2}+\cdots+\left(a_{n}-b_{n}\right)^{2}}= \sqrt{\sum_{i=1}^{n}\left(a_{i}-b_{i}\right)^{2}} \end{array}.\]
Cosine Similarity
\(a \cdot b=\|a\|\|b\| \cos \theta\) \[\text { similarity }=\cos (\theta)=\frac{A \cdot B}{\|A\|\|B\|}=\frac{\sum_{i=1}^{n} A_{i} \times B_{i}}{\sqrt{\sum_{i=1}^{n}\left(A_{i}\right)^{2}} \times \sqrt{\sum_{i=1}^{n}\left(B_{i}\right)^{2}}}\]
[-1, 1]의 범위를 가집니다. 1이면 x와 y는 동일 -1이면 x와 y는 반대 0이면 x와 y는 독립 임을 뜻합니다.
scale에 대한 고려를 하지 않는다는 문제점이 있습니다. 또한, 다양한 차원이 존재하면 유사도를 잘 나타낼 수 있지만 항목이 1개인 경우, 즉 1차원일 경우 항상 1이 나온다는 단점이 있습니다. 1차원에서는 각도를 고려할 수 없기 때문입니다.
Jaccard Similarity
\(J(A, B)=\frac{\mid A \cap B\mid}{\mid A \cup B\mid}=\frac{\mid A \cap B\mid}{\mid A\mid +\mid B\mid-\mid A \cap B\mid}\)
집합의 개념을 사용합니다. 공통 Item이 없으면 0, 모두 겹치면 1의 결과가 나옵니다.
Pearson Correlation(Similarity)
양적 변수들 사이의 선형관계를 확인하기 위한 방법으로 자주 쓰이는 방법입니다. 코사인 유사도와 매우 유사한 계산 방법이지만, x와 y에서 각각의 평균값을 빼 주어 공분산으로 계산을 하고 있습니다. \[r_{x y}=\frac{\sum_{i}^{n}\left(X_{i}-\bar{X}\right)\left(Y_{i}-\bar{Y}\right)}{\sqrt{\sum_{i}^{n}\left(X_{i}-\bar{X}\right)^{2}} \sqrt{\sum_{i}^{n}\left(Y_{i}-\bar{Y}\right)^{2}}}\]
코사인 유사도와 마찬가지로 scale에 대한 고려를 하지 않습니다. 다만 평균값을 기준으로 한 편차를 사용하기 때문에 변수 간의 절대적인 크기(scale)가 아닌 상대적인 변화율이 고려되며, scale 조정을 가능하게 해줍니다.
RecSys의 평가
RecSys의 성능을 평가하는 방법으로는 크게 두 가지가 있습니다.
- Root Mean Square Error(RMSE)
- Normalized Discounted Cumulative Gain(NDCG)
Root Mean Square Error(RMSE)
: 평균 제곱근 편차 \(RMSE = \sqrt{\frac{1}{n}\sum{^n_{i=1}}(y_i-\hat y_i)^2}\) 실제 값과 모델의 예측 값의 차이를 하나의 숫자로 나타낼 수 있습니다. “차이” 이기 때문에 결과값이 작을수록 추천 알고리즘의 성능이 좋다고 판단합니다. 예측 task의 성능을 평가할 때 주로 사용됩니다. 예측 대상 값에 영향을 받습니다.(Scale-Dependent)
- 1~10점의 평점을 갖는 A플랫폼과 1~100점의 평점을 갖는 B플랫폼은 같은 RMSE값이 나와도 같은 성능이라고 볼 수 없습니다.
Normalized Discounted Cumulative Gain(NDCG)
이 평가방법은 랭킹 task의 성능을 평가할 때 주로 사용됩니다. NDCG는 세 단계에 걸쳐 이루어집니다.
관련성 점수(Relevance Score)를 계산합니다. \(= CG_p\) \(CG_p=\sum^p_{i=1}rel_i\) 사용자가 추천된 아이템을 얼마나 선호하는지를 나타내는 점수 \(rel_i\)를 상위 아이템 p개에 대해 동일한 비중으로 합한 값입니다. i가 1이면 랭킹 1위의 아이템일 것입니다.
Discount를 적용합니다. \(= DCG_p\) \(DCG_p=rel_1+\sum^p_{i=2}\frac{rel_i}{log_2i}\) 개별 아이템의 관련성에 log normalization을 적용합니다. 랭킹에 따라 비중을 discount해서 관련성을 계산합니다. 랭킹이 낮아질수록 비중이 적어지는 페널티를 받게 됩니다.
Normalization을 진행합니다. \(= NDCG_p\) \(NDCG_p=\frac{DCG_p}{IDCG_p}\) IDCG는 전체 p개의 결과 중 가질 수 있는 가장 큰 DCG값입니다.
이로써 최종적으로 Normalized된 NDCG 평가지표를 구할 수 있습니다. NDCG는 0~1사이의 값을 가지며, 1에 가까울수록 추천 알고리즘의 성능이 좋다고 판단합니다.
출처: https://seunghan96.github.io/rs/1.Introduction-to-Recommender-System/
